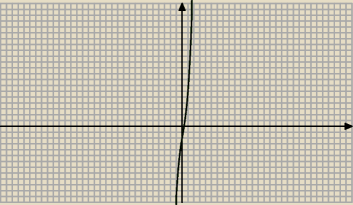
okkk pies: 3x³−x²+6x−2≤0 (x²+2)(3x−1)≤0 x=1/3 −>przecina wyk. i odp jest x∊(−00,1/3> −>tego nie rozumiem dlaczego tak jest wpislalem do programu i mi narysowlo...ale dlaczego od dolu skoro wielomian zaczna sie od liczby dodtniej

yyhy: (x²+2)(3x−1)≤0

	1		1
czyli 3x−1≤0 czyli 3x≤1 czyli x≤		czyli x∊(−∞,		)
	3		3

pies: nie rozumiem

yyhy: czego?

pies: pezeciez wykres wielomianu rysuje sie zaczynajac od dolu albo gory

pies: https://matematykaszkolna.pl/strona/142.html

yyhy: KIedy wykres jest poniżej osi y=0 ?

pies: nie weim co to znaczy rysuje wykres .. zaczynajac od prawej strony ? czyli od konca?

yyhy: Zaczynasz rysowaj od prawej sttorny (od góry) , przecisz w x=1/3 i rysujesz w dół.. (bo potęga jest nieparzysta=1)

yyhy: Jkaby było (x²+2)(3x−1)² to byś odbił i znów do góry

PW: "dlaczego od dołu, skoro wielomian zaczyna się od liczby dodatniej". Wielomian ma dodatni współczynnik przy najwyższej potędze, przy x³ stoi dodatnia liczba 3. I w porządku, mówiąc "po chłopsku" w definicji wielomianu dominują liczby 3x³, one najwięcej znaczą. A 3x³ jest ujemne dla x < 0. Bardziej formalnie:

	1		2		2
(1) 3x3 − x2 + 6x − 2 = 3x3(1 −		+		−		)
	3x		x2		3x3

− widać, że wyrażenie w nawiasie niewiele różni się od 1 dla dostatecznie dużych co do wartości bezwzględnej x, granica wyrażenia w nawiasie dla x→−∞ lub dla x→+∞ jest równa 1, zatem dla "dużych x" znak wielomianu jest taki jak znak czynnika 3x³.

pies: dzieki yhy ..PW ja z tego nic nie rozumiem ...

Qulka: w punkcie 5 linka co podałeś na zielono..od PRAWEJ zaczynasz i jedziesz do tych punktów co zaznaczyłeś jako miejsca zerowe u Ciebie od prawej od góry i masz rys

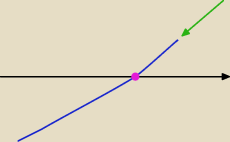
Qulka: od prawej od góry (zielona strzałka) i tylko jeden punkt więc dalej w dół

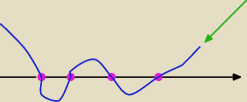
Qulka: ale gdyby było więcej miejsc zerowych to idziesz wężykiem (powiedzmy że nie ma parzystokrotnych)

PW: pies, weź wzór (1) z 17:41 i podstaw x = −10, potem x = −100, x = −1000 (nie musisz dokładnie liczyć, ale przekonaj się, że rzeczywiście 3 ostatnie ułamki po prawej stronie niewiele znaczą, a więc wartość wielomianu jest ujemna, bo ujemne jest 3x³. To jest intuicyjne uzasadnienie, dlaczego rysujemy "od dołu od lewej", czyli dlaczego wielomian ma wartości ujemne dla x ujemnych o dużej wartości bezwzględnej. Nie wolno tak podchodzić do problemów, że po trzech minutach mówi się "ja z tego nic nie rozumiem".

PW: Qulka, wyczytałem gdzie indziej, że zamierzasz pisać książkę. Życzę Ci wytrwałości, bo rzecz jest trudna. Wszyscy wiemy, że czym innym jest rozwiązanie problemu, a czym innym zapisanie rozwiązania tak, by samo się broniło. W moim wykonaniu złożenie do druku jednego rozwiązania zadania przekraczało 1 dzień mozolnej pracy. Jaka szkoda, że ślepnę, już miałem gotowe do druku (sam byłem zecerem) 100 trudnych zadań rozwiązanych "łopatologicznie i na 3 sposoby", gdy zorientowałem się o przywróceniu do programu rachunku różniczkowego. Na dalsze 50 zadań już nie mam siły, książkę w 1 egzemplarzu zostawię wnukom.

Qulka: PW ..zadania maturalne na podstawę były tak napisane, że się same broniły bo naprawdę ich celem było nauczenie korzystania z tablic, żeby przyszli studenci umieli czytać skrypty, ale w tym roku niestety pozmieniali