ekstrema brick: Jakie powinny być długości przekątnych deltoidu o bokach a i b, aby jego pole było największe? Mam problem z tym zadaniem, bo nie za bardzo wiem, jak uzależnić długość chociaż jednej przekątnej od długości boków. Proszę o pomoc.

Kacper: Podaj pełną treść zadania, bo brakuje informacji.

brick: To są wszystkie dane, przekątne to p i q. Dane są a i b.

brick:

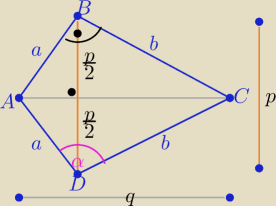
Eta: Pole deltoidu= a*b*sinα −−−− jest największe,jeżeli sinα =1 ⇒ α=90^o

	p*q		2ab
to P=a*b i P=		⇒ p*q=2ab ⇒ p=
	2		q

z tw. Pitagorasa w trójkącie ABC

	2ab
q2=a2+b2 ⇒ q= √a2+b2 i p=
	√a2+b2

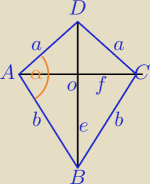
iryt: BD=e, AC=f P_ABCD=a*b*sinα, α∊(0,π)

	e*f
PABCD=
	2

	π
P=a*b*sinα jest największe dla α=
	2

wtedy: ΔBAD− Δprostokątny, P_ABCD=a*b e²=a²+b²⇔e=√a²+b²

	e*f
a*b=
	2

	√a2+b2
a*b=		*f
	2

	2ab
f=
	√a2+b2

e=√a²+b² ============= ?

brick: Ogromne podziękowania dla Was! Dziękuję!

Mila:

Eta: