Wykazać bnyh6: Wykazać , że spośród wszystkich trójkątów prostokątnych o przeciwprostokątnej o długości c, największe pole ma trójkąt równoramienny.

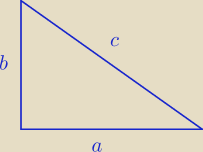
Janek191: a² + b² = c² ⇒ b² = c² − a² ⇒ b = √c² − a² Pole Δ P = 0,5 a*b = 0,5 a*√c² − a² więc

	0,5 a
P '(a) = 0,5√c2 − a2 +		*( − 2 a) =
	2 √c2 − a2

	0,5 a2		a2
=0,5 √c2 −a2 −		= 0 ⇔ √c2 −a2 =		⇔
	√c2 − a2		√c2 − a2

	c2 − a2		a2
⇔		=		⇔ c2 − a2 = a2 ⇔ c2 = 2 a2⇔
	√c2 − a2		√c2 − a2

	c
⇔ c = √2 a ⇔ a =
	√2

	c
wtedy b = √c2 − 0,5 c2 = √0,5*c =
	√2

a = b

kochanus_niepospolitus:

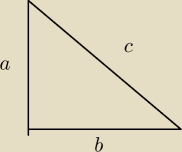
	ab
ogólny wzór na pole trójkąta:
	2

z tw. Pitagorasa: c² = a² + b² −> b² = c²−a² −> b = √c²−a²

	ab		a√c2−a2
PΔ =		=
	2		2

liczysz maksimum P_Δ(a)