Planimetria bartek: Z wierzchołków prostokąta poprowadzono proste prostopadłe do jego przekątnej.Proste te dzielą przekątna na trzy równe części ,każda o długości 5 cm. Oblicz pole i obwód tego prostokąta.

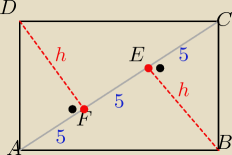
Li : IACI=15

	IAFI		IDFI
ΔAFD ~ ΔFCD to:		=
	IDFI		IFCI

to IDFI²=IAFI*IFCI= 5*10= 50 to: IDFI= h= √50= 5√2 cm Pole P( ABCD}= 2*P(ΔACD)= 2*¹₂*15*5√2= 75√2 cm² z tw. Pitagorasa w Δ AFD : IADI² = 5² +(5√2)² = 25+50 = 75 to: IADI= 5√3 cm z tw. Pitagorasa w ΔACD: IDCI²= 15² − (5√3)² = 225 − 75= 150 IDCI= √150= √25*6= 5√6 cm Ob= 2*5√2+2*5√6= 10√2 +10√2*√3= 10√2( 1+√3) cm

Jolanta: Podziwiam ten rysunek

Kornel: Czy przypadkiem nie przepisałeś źle boku |AD| do obliczania obwodu ? Jest 5√2 zamiast 5√3. I powinno wyjść na końcu 10√3(√3 + 1)

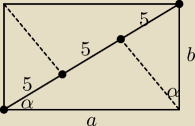
Bogdan: Korzystając z podobieństwa trójkątów podobnych otrzymujemy:

10		a
	=		⇒ a = 5√6
a		15

5		b
	=		⇒ b = 5√3
b		15

olga:

pieseł: πδ≈≠∫∊≥≤∞Ω→⇔

madga : δΩπβαγδℂ