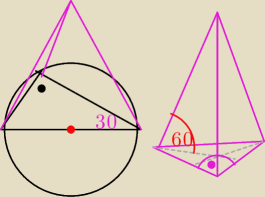
bryła wpisana w bryłę Archeolog: Podstawą ostrosłupa jest trójkąt prostokątny o kącie ostrym 30 stopni. Każda krawędź boczna jest nachylona do płaszczyzny podstawy pod kątem 60 stopni. Oblicz stosunek objętości ostrosłupa do objętości opisanej na nim kuli. No więc oznaczyłem sobie przeciwprostokątną podstawy 2c i wyszło mi,że H = √3*c.

	√3*c2		3*c3
Pole podstawy wyszło mi :		i w sumie objętość tej figury V =		.
	2		2

Coś źle obliczyłem? Wynik nie wychodzi taki jak mam w odpowiedziach. Objętość kuli podstawiłem c jako promień (bo inaczej podstawa nie mogłaby być w nią wpisana?)

	4*c3*π
do wzoru. V(kula) =		.
	3

Prosiłbym o pokazanie błędu jeśli jakiś jest i naprowadzenie na dobrą ścieżkę

dero2005: https://matematykaszkolna.pl/forum/315426.html

Jack: gg ?

Archeolog: teraz tamten obrazek to mnie tak zmylił, że ja już nic nie wiem... czyli nic nie jest promieniem kuli

dero2005:

	2
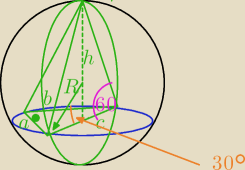
promieniem kuli jest R =		a√3 gdzie a − krótsza przyprostokątna podstawy
	3

Archeolog: a z czego to wynika?

dero2005:

	2
bo to jest		wysokości ostrosłupa
	3

dero2005:

Archeolog: 60, 60, 60... równoboczny... faktycznie dostosowałem sobie dane (ja przyjąłem, że przeciwprostokątna = 2c) i ładnie wyszło dzięki wszystkim