Symetria srodkiwa krzywych
Yazz: Wyznxz równanie krzywej będącej obrazem krzywej o podanym rownaniu w symetrii środkowej
względem Ś.
Y=1/x, S(5,−1)
Y=2/x+1, S(−2,4)
11 lut 20:53
Qulka:
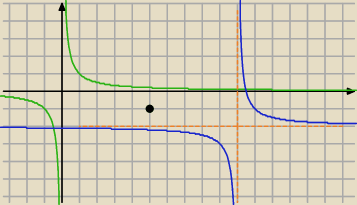
11 lut 21:02
Yazz: Nie chcę odpowiedzi

ani nie za bardzo rysować takie coś na wykresie i odczytywać − bo
takiego nie narysowałbym na kartce, nie chciałoby mi się nawet próbować.
Na 99% jest jakiś sposób na wyliczenie tego :x
11 lut 21:04
Qulka:
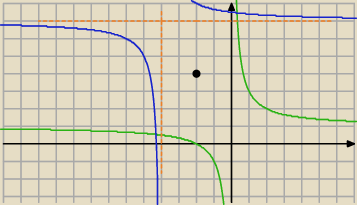
11 lut 21:06
Qulka: jak się przyjrzysz to może się domyślisz

jest o tyle łatwo że te wykresy są symetryczne wzg własnego środka

11 lut 21:08
Yazz: =.=
11 lut 21:08
Yazz: Kurde, jestem trochę zmęczony :v
11 lut 21:10
11 lut 21:11
Yazz: Czyli trzeba w tym wypadku przesunąć wykres funkcji o podwojony wektor OS gdzie O to (0,0)?
Mówię o pierwszym.
11 lut 21:13
Qulka: tak
11 lut 21:14
Yazz: W drugim wypadku, o podwojony wektor OS gdzie O jest (0,1)
11 lut 21:18
Qulka: jak widać
11 lut 21:18
Yazz: Dobra, dziękuję : )
11 lut 21:21
Mila:
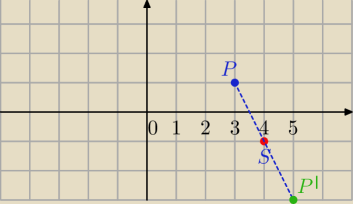
P(x,y) − dowolny punkt płaszczyzny
P'(x',y') obraz punktu P po przekształceniu:
S =(5,−1) środek symetrii
S jest środkiem PP'
| | x+x' | |
5= |
| ⇔10=x+x'⇔x'=10−x |
| | 2 | |
| | y+y' | |
−1= |
| ⇔−2=y+y'⇔y'=−2−y |
| | 2 | |
Przekształcamy krzywa wg wzoru:
x'=10−x
y'=−2−y
Obliczymy x i y i wstawimy do wzoru : x=10−x', y=−2−y'
| | 1 | |
y'= |
| −2 opuszczamy znaczki: |
| | x'−10 | |
===========
Ogólnie wzór:
Symetria środkowa względem S=(a,b)
Punkt P=(x,y) po przekształceniu ma współrzędne:
x'=−x+2a
y'=−y+2b
11 lut 21:26

 ani nie za bardzo rysować takie coś na wykresie i odczytywać − bo
takiego nie narysowałbym na kartce, nie chciałoby mi się nawet próbować.
Na 99% jest jakiś sposób na wyliczenie tego :x
ani nie za bardzo rysować takie coś na wykresie i odczytywać − bo
takiego nie narysowałbym na kartce, nie chciałoby mi się nawet próbować.
Na 99% jest jakiś sposób na wyliczenie tego :x

 jest o tyle łatwo że te wykresy są symetryczne wzg własnego środka
jest o tyle łatwo że te wykresy są symetryczne wzg własnego środka 
 P(x,y) − dowolny punkt płaszczyzny
P'(x',y') obraz punktu P po przekształceniu:
S =(5,−1) środek symetrii
S jest środkiem PP'
P(x,y) − dowolny punkt płaszczyzny
P'(x',y') obraz punktu P po przekształceniu:
S =(5,−1) środek symetrii
S jest środkiem PP'