Przekątna graniastosłupa prawidłowego czworokątnego jest nachylona do podstawy krystian prosi o pomoc: Zad. 1: a) Przekątna graniastosłupa prawidłowego czworokątnego jest nachylona do podstawy pod kątem 30stopni , a przekątna ściany bocznej ma długość d. Oblicz pole powierzchni tego graniastosłupa. b) Oblicz objętość graniastosłupa prawidłowego sześciokątnego, którego krótsza przekątna ma długość d , a dłuŜsza przekątna jest nachylona do płaszczyzny podstawy pod kątem 60stopni.

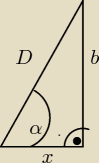
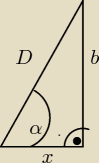Jolanta: Zad1. a) Pc=Pb+2Pp Pb=4*a*b Pp=a² a− krawędź podstawy, b − wysokość d − przekątna ściany bocznej. Tw.Pitagorasa 1) a²+b²=d² Następnie D− przekątna graniastosłupa x− przekątna podstawy x=a√2 tg30^o = ^b_x = ^b_a√2 2) √3/3 = b/(a√2) Zatem otrzymujemy układ równań: a²+b²=d² √3/3 = b/(a√2) gdzie d jest dane natomiast a,b − szukane. (2/3)a² + a² = d² a²=(3/5)d², to a=√15/5d b²=d²−a² b²=(2/5)d², to b²=√10/5d. Więc Pc=4*(√6/5)*d²+2*(3/5)*d² Pc=(4√6+6)*d²/5 − na pewno dobrze zad1b) Zapiszę tylko najważniejsze zależności. H − wysokość graniastosłupa a − krawędź podstawy h − wysokość trójkąta równobocznego (sześciokąt w podstawie jest zbudowany z takich 6 trójkątów ) d − krótsza przekątna D − dłuższa przekątna z trójkąta prostokątnego o bokach H,D,2*a tg60^o=H/(2*a) z trójkąta prostokątnego o bokach H,d,2*h Tw. Pitagorasa H²+(2h)²=d² Pamiętając,że h=(a√3)/2 w trójkącie równobocznym rozwiążesz dalej to zadanie. Powodzenia.