wielomiany parametr
ktoś: Dla jakich wartości parametru m (m∊R) równanie
x
4+(m+1)x
2+m
2+6m+9=0
x
2=t
I teraz jakie warunki? Wpadłem na Δ=0, tylko jak wykluczyć aby te rozwiązanie nie było ujemne
ani zerowe? Viete'a można w takiej sytuacji dać? Bo mam mętlik i nie pamiętam już czy on
działa w sytuacji gdy Δ=0. Możliwe, że coś namieszałem bo robię już kilka godzin zadania
11 lut 19:43
azeta: ale dla jakich wartości parametru równanie, co? jest żyrafą?
przepisz dokładnie polecenie,
wtedy coś pomyślimy
11 lut 19:46
Jerzy:
a jaka treśc zadania ?
11 lut 19:46
ktoś : Ups, ma 2 rożne rozwiązania
11 lut 19:55
ktoś : Trzeba sprawdzić po prostu −b/2a≠0
11 lut 19:56
ktoś : Ehh, te pisanie z telefonu. Na końcu mial byc znak zapytania :s
11 lut 19:56
Mila:
Dla jakich wartości parametru m (m∊R) równanie:
(*) x
4+(m+1)x
2+m
2+6m+9=0 ma dwa różne rozwiązania?
x
2=t, t≥0
(**) t
2+(m+1)*t+m
2+6m+9
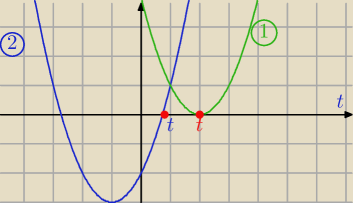
1) Aby równanie (*) miało dokładnie dwa pierwiastki, równanie kwadratowe (**)
musi mieć dokładnie jeden pierwiastek dodatni.
Sytuacja na rysunku− tak może wyglądać wykres f(t)
2) Sprawdźmy kiedy równanie ma pierwiastki.
Δ=(m+1)
2−4*(m
2+6m+9)=m
2+2m+1−4m
2−24m−36=−3m
2−22m−35
(1) Δ=0 i t>0
−3m
2−22m−35=0
Δ
m=484−420=64
Obliczymy pierwiastek :
m=−5
| | −b | | m+1 | | −5+1 | |
t= |
| =− |
| =− |
| =2 >0 ⇔x2=2 i masz dwa różne pierwiastki równania (*) |
| | 2a | | 2 | | 2 | |
=====
| | | | 2 | |
t= |
| = |
| >0 i masz dwa różne pierwiastki równania (*) |
| | 2 | | 3 | |
(2) rozważamy drugą sytuację:
Δ>0
i
t
1*t
2<0
Policzysz sam?
11 lut 21:00
ktoś: Warunki starczą mi
Czyli po podstawieniu t
Δ=0 i −b/2a>0
lub
Δ>0 i t1t2*<0
Dobrze rozumiem?
11 lut 21:22
ktoś: Δ>0
i
t1*t2<0
Chociaż ta sytuacjia nieco mnie nurtuje. Jak t1 lub t2 ma być ujemne gdy oba są kwadratami
(x2)? Wątpie by było to możliwe, więc chyba pozostanie warunek Δ=0 i −b/2a>0
11 lut 21:34
Qulka: właśnie dlatego że jeden jest ujemny zostają dwa rozwiązania zamiast 4
bo pozostałe dwa są w zbiorze liczb zespolonych
11 lut 21:41
ktoś: Emm, w takim wypadku powinienem dawać ten warunek będąc na poziomie liceum?
11 lut 21:44
Mila:
Drugie równanie nie wie o tym założeniu.
Zobacz co otrzymasz?
Wtedy dopiero wykluczasz.
11 lut 21:44
Qulka: tak powinieneś .. bo na poziomie liceum mówi się wówczas o dwóch rozwiązaniach
11 lut 21:45
ktoś: To w w warunku Δ>0 i t1t2*<0 i tak wyjdzie zbiór pusty
11 lut 21:49
Mila:
Wyjdzie. Ale gdyby np. c=m2−1 to byłaby inna sytuacja .
11 lut 22:15