Obw. trójkąta
nick: Promień okręgu opisanego na trójkącie prostokątnym jest równy R, a promień okręgu wpisanego w
ten trójkąt wynosi r. Ile wynosi obwód tego trójkąta?
11 lut 17:53
Eta:
a+b=2r+2R , c= 2R
L=a+b+c= 4R+2r
11 lut 18:22
===:
4R+2r
11 lut 18:38
Eta:
11 lut 18:41
Eta:
@
=== po 16 min ..... przepisać mój wynik !
11 lut 18:42
Agata: Dziękuję, a skąd wiemy, że a+b=2r+2R?
11 lut 18:43
Eta:
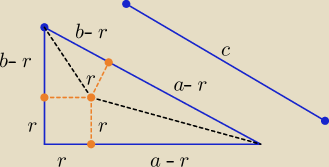
c=2R
c= a−r+b−r ⇒ 2R= a+b−2r ⇒ a+b=2R+2r
11 lut 18:47
Eta:
| | a+b−c | |
Lub ze wzoru z tablic : c=2R i r= |
| ⇒ 2r=a+b−2R ⇒ a+b=2r+2R |
| | 2 | |
11 lut 18:48
===:
oj
ECINKA Wnuki mają swoje prawa
11 lut 18:50
===:
ale na dowód, że nie przepisałem podam inne rozwiązanie
Że a
2+b
2=4R
2 to oczywistość
(a+b)
−2ab=4R
2
(a+b)
2−4R
2=2ab a nasze 2ab to 4P (4 pola trójkąta)
(a+b+2R)(a+b−2R)=2ab
| | 2P | |
r= |
| ⇒ 2P=r(a+b+2R) |
| | a+b+2R | |
4P=2r(a+b+2R)
(a+b+2R)(a+b−2R)=2r(a+b+2R)
a+b−2R=2r
a+b+2R=2r+4R
11 lut 19:05
===:
i jeszcze z literówką
w trzeciej linijce oczywiście (a+b)
2−2ab=4R
2
11 lut 19:07