 I sposób:
Ponieważ w obu urnach masz po 4 czarne kule, a możliwość wybrania każdej urny jest jednakowa,
to nie komplikując sobie życia można rozważyć rozkłady kul:
U1 U2
4C,1B 4C 5B
lub
4C, 2B 4C 4B
4C, 3B 4C,3B
Obliczyc prawd. i porównać.
==================
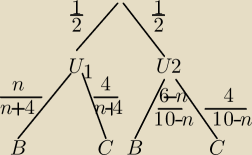
II sposób
U1 4+n kul
U2 4+6−n kul
0≤n≤6
I sposób:
Ponieważ w obu urnach masz po 4 czarne kule, a możliwość wybrania każdej urny jest jednakowa,
to nie komplikując sobie życia można rozważyć rozkłady kul:
U1 U2
4C,1B 4C 5B
lub
4C, 2B 4C 4B
4C, 3B 4C,3B
Obliczyc prawd. i porównać.
==================
II sposób
U1 4+n kul
U2 4+6−n kul
0≤n≤6
| 1 | n | 1 | 6−n | |||||
P(B)= | * | + | * | = | ||||
| 2 | n+4 | 2 | 10−n |
| 1 | n*(10−n)+(6−n)*(n+4) | −n2+6n+12 | ||||
= | *( | = | ||||
| 2 | (n+4)*(10−n) | −n2+6n+40 |
| −28 | ||
=1+ | ⇔ | |
| −n2+6n+40 |
| 28 | ||
P(B)=1+ | ||
| n2−6n−40 |
| 28 | 21 | 3 | ||||
P(B)=(1+ | )= | = | ||||
| −49 | 49 | 7 |