Okrąg Dankos: Z punktu A odległego od środka okręgu o ³₂ promienia r poprowadzono prostą styczną do okręgu. Udowodnij, że odległość punktu A od punktu styczności prostej i okręgu jest równa ^r√5₂

Eta:

	3
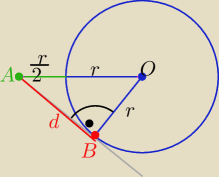
|AO|=		r , |BO|=r , |AB|=d
	2

|∡ABO|= 90^o , bo prosta AB jest styczna do okręgu w punkcie B z twierdzenia Pitagorasa w ΔOAB

	3		9		5		r
d=√(		r)2−r2= √		r2−r2= √		r2 =		√5
	2		4		4		2