| x | 2pi | √3 | ||||
sin( | − | )>=− | ||||
| 3 | 3 | 2 |
| 4pi | x | 2pi | 5pi | ||||
+2kpi<= | − | <= | +2kpi | ||||
| 3 | 3 | 3 | 3 |
| x | 2pi | √3 | ||||
cos( | − | )>=− | ||||
| 3 | 3 | 2 |
| pi | x | 2pi | 11pi | ||||
+2kpi<= | − | <= | +2kpi | ||||
| 6 | 3 | 3 | 6 |
| 3pi | 7pi | |||
− | +6kpi<=x<= | +6kpi | ||
| 2 | 2 |
| x | 2pi | 1 | ||||
cos( | − | )>=− | ||||
| 3 | 3 | 2 |
| 2pi | x | 2pi | 4pi | ||||
+2kpi<= | − | <= | +2kpi | ||||
| 3 | 3 | 3 | 3 |
| pi | 1 | |||
sin(−2x+ | )=− | |||
| 3 | 2 |
| 1 | 5pi | 4pi | pi | pi | ||||||
a to jak ? skoro sin − | = | v | a sin jest od <− | > | ||||||
| 2 | 3 | 3 | 2 | 2 |
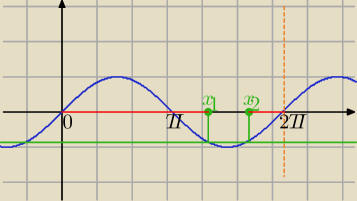
| x | 2π | √3 | ||||
sin( | − | )≥− | ||||
| 3 | 3 | 2 |
| √3 | ||
Rozważasz kiedy wykres leży nad prostą y=− | ||
| 2 |
| π | π | |||
x1=π+ | , x2=2π− | |||
| 3 | 3 |
| 4π | 5π | |||
x1= | , x2= | |||
| 3 | 3 |
| x | 2π | 4π | 5π | x | 2π | 2π | ||||||||
0+2kπ≤ | − | ≤ | +2kπ lub | +2kπ≤ | − | ≤2π+2kπ /+ | ⇔ | |||||||
| 3 | 3 | 3 | 3 | 3 | 3 | 3 |
| 2π | x | 6π | 7π | x | 8π | ||||||
+2kπ≤ | ≤ | +2kπ lub | +2kπ≤ | ≤ | +2kπ /*3 | ||||||
| 3 | 3 | 3 | 3 | 3 | 3 |