Bogdan:
Pomijam w zapisach znak →
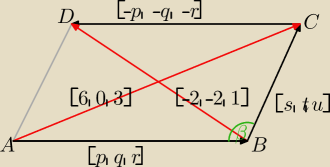
Suma wektorów: AB + BC = AC ⇒ [p + s, q + t, r + u] = [6, 0, 3]
Suma wektorów: BC + CD = BD ⇒ [−p + s, −q + t, −r + u] = [−2, −2, 1]
p + s = 6 i −p + s = −2 ⇒ p = 4 i s = 2
q + t = 0 i −q + t = −2 ⇒ q = 1 i t = −1
r + u = 3 i −r + u = 1 ⇒ r = 1 i u = 2
Wektor AB = [4, 1, 1], wektor BC = [2, −1, 2]
Długości tych wektorów: |AB| =
√16 + 1 + 1 = 3
√2, |BC| =
√4 + 1 + 4 = 3
Iloczyn skalarny wektorów AB i BC: AB◯BC = 4*2 − 1*1 + 1*2 = 9 i AB◯BC = 3
√2 * 3 * cosβ
9
√2 cosβ = 9 ⇒ cosβ = ... ⇒ β = ...
 Pomijam w zapisach znak →
Suma wektorów: AB + BC = AC ⇒ [p + s, q + t, r + u] = [6, 0, 3]
Suma wektorów: BC + CD = BD ⇒ [−p + s, −q + t, −r + u] = [−2, −2, 1]
p + s = 6 i −p + s = −2 ⇒ p = 4 i s = 2
q + t = 0 i −q + t = −2 ⇒ q = 1 i t = −1
r + u = 3 i −r + u = 1 ⇒ r = 1 i u = 2
Wektor AB = [4, 1, 1], wektor BC = [2, −1, 2]
Długości tych wektorów: |AB| = √16 + 1 + 1 = 3√2, |BC| = √4 + 1 + 4 = 3
Iloczyn skalarny wektorów AB i BC: AB◯BC = 4*2 − 1*1 + 1*2 = 9 i AB◯BC = 3√2 * 3 * cosβ
9√2 cosβ = 9 ⇒ cosβ = ... ⇒ β = ...
Pomijam w zapisach znak →
Suma wektorów: AB + BC = AC ⇒ [p + s, q + t, r + u] = [6, 0, 3]
Suma wektorów: BC + CD = BD ⇒ [−p + s, −q + t, −r + u] = [−2, −2, 1]
p + s = 6 i −p + s = −2 ⇒ p = 4 i s = 2
q + t = 0 i −q + t = −2 ⇒ q = 1 i t = −1
r + u = 3 i −r + u = 1 ⇒ r = 1 i u = 2
Wektor AB = [4, 1, 1], wektor BC = [2, −1, 2]
Długości tych wektorów: |AB| = √16 + 1 + 1 = 3√2, |BC| = √4 + 1 + 4 = 3
Iloczyn skalarny wektorów AB i BC: AB◯BC = 4*2 − 1*1 + 1*2 = 9 i AB◯BC = 3√2 * 3 * cosβ
9√2 cosβ = 9 ⇒ cosβ = ... ⇒ β = ...