sześcian Kaś;*: Wykaż, że płaszczyzna przechodząca przez wierzchołki A',B,C' dzieli przekątną sześcianu DB' w stosunku 1:2

ANNA: pomagam

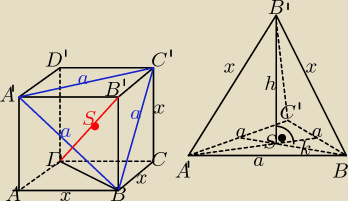
ANNA: Po przecięciu sześcianu daną płaszczyzną, odcięta część jest ostrosłupem prawidłowym trójkątnym. Z ΔSBB' w ostrosłupie wyznaczam h za pomocą x : h² + k² = x²

	2		a√3
h2 + (		*		)2 = x2
	3		2

	a√3
h2 + (		)2 = x2
	3

a = x√2 (przekątna kwadratu), zatem:

	x√2*√3
h2 + (		)2 = x2
	3

	2
h2 +		x2 = x2
	3

	x2		x		x√3
h2 =		⇒ h =		=
	3		√3		3

Z ΔDBB' w sześcianie obliczam długość jego przekątnej DB' : IDB'I² = x² + (x√2)² IDB'I² = x² + 2x² IDB'I² = 3x² ⇒ IDB'I = x√3 Przecinająca płaszczyzna przecięła przekątną DB' na odcinki DS i SB'.

	x√3		2
IDSI = IDB'I − h = x√3 −		=		x√3
	3		3

	ISB'I		h
Wyznaczam żadany stosunek:		=		=
	IDSI		IDSI

	x√3		2x√3		1
=		:		=		= 1 : 2
	3		3		2

Li : Można też tak V _sześcianu= x³ to: V_ostr= ¹₆*x³ ponad to V _ostr= ¹₃*P_ΔBC^'A^'*IB^'SI , gdzie IB^'SI −−− dł. wysokości ostrosłupa trójkąt BC^'A^' jest równoboczny o boku długości x√2 to

	(x√2)2*√3		x2√3
PΔBC'A/=		=
	4		2

zatem:

	x2√3
16x3= 13*		*IB'SI
	2

	x√3
to IB'SI=
	3

d_sześcianu= x√3 więc IB^'SI = ¹₃d_sześcianu to: ISDI= ²₃d{sześcianu zatem:

	IB'SI		1
		= 13:23= 13*32=
	ISDI		2

to podział jest w stosunku 1: 2