Dziedzina funkcji
xaxex: Wyznacz dziedzinę funkcji
−3(x−1)2x3(x−2)4(x+2)>0
Trzeba zrobić jakiś wykres i na nim pozaznaczać miejsca zerowe i tam gdzie jest parzysta miejsc
zerowych to funkcja się "odbija", a nieparzysta to idzie na dół, ale dokładnie nie wiem jak to
zrobić.
10 lut 13:52
Jerzy:
D = R ...i koniec zadania
10 lut 13:54
xaxex: W rozwiązaniu mam od −2,0, zresztą chodzi o to w jaki sposób się to rozwiązuje, bo takie
zadanie było na egzaminie, a się przygotowuję do następnego terminu.
10 lut 13:56
kochanus_niepospolitus:
xaxex napisałeś polecenie WYZNACZ DZIEDZINE FUNKCJI a podajesz nierówność wielomianową

Czy to jest 'skrót myślowy' (np taki oto wielomian jest pod pierwiastkiem w mianowniku?) Czy
też treść jest z innego zadania?
10 lut 14:01
omg: boż śwęty
kochanus coś tm coś tam co Ty taki wrażliwy


?
10 lut 14:02
xaxex: Ta funkcja po prostu była w logarytmie, dlatego zrobiłem skrót i od razu zrobiłem, że ma być
większe niż 0.
10 lut 14:05
kochanus_niepospolitus:
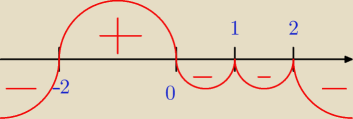
a więc uczymy się zasady 'rysowania wężyka'
1) rysowanie wężyka zaczynam od narysowania linii (reprezentuje ona oś OX)
2) zaznaczymy wszystkie miejsca zerowe (czyli −2 , 0 , 1 , 2)
3) rysowanie zaczynać będzie od PRAWEJ STRONY

4) rysowanie zaczynam od góry JEŻELI a>0 ; a od doły JEŻELI a<0 (w naszym przypadku będzie od
dołu bo a = −3 <0)
5) 'dociągamy' do pierwszego miejsca zerowego (x=2) które jest parzyste, więc 'odbijamy (wąż
zostaje po 'dolnej' czyli 'ujemnej' stronie)
6) dociągamy do drugiego miejsca zerowego (x=1), które także jest parzystego stopnia, więc
'odbijamy'
7) 'dociągamy' do kolejnego miejsca zerowego (x=0), które jest nieparzystego stopnie, więc
'przechodzimy' przez oś na część górną (dodatnią)
8) dociągamy do kolejnego miejsca zerowego (x=−2), które jest nieparzystego stopnia, więc
'przechodzimy' przez oś
9) nie ma więcej miejsc zerowych, więc 'puszczamy węża' w nieskończoność
10 lut 14:19
10 lut 14:25
 Czy to jest 'skrót myślowy' (np taki oto wielomian jest pod pierwiastkiem w mianowniku?) Czy
też treść jest z innego zadania?
Czy to jest 'skrót myślowy' (np taki oto wielomian jest pod pierwiastkiem w mianowniku?) Czy
też treść jest z innego zadania?

 ?
?
 a więc uczymy się zasady 'rysowania wężyka'
1) rysowanie wężyka zaczynam od narysowania linii (reprezentuje ona oś OX)
2) zaznaczymy wszystkie miejsca zerowe (czyli −2 , 0 , 1 , 2)
3) rysowanie zaczynać będzie od PRAWEJ STRONY
a więc uczymy się zasady 'rysowania wężyka'
1) rysowanie wężyka zaczynam od narysowania linii (reprezentuje ona oś OX)
2) zaznaczymy wszystkie miejsca zerowe (czyli −2 , 0 , 1 , 2)
3) rysowanie zaczynać będzie od PRAWEJ STRONY  4) rysowanie zaczynam od góry JEŻELI a>0 ; a od doły JEŻELI a<0 (w naszym przypadku będzie od
dołu bo a = −3 <0)
5) 'dociągamy' do pierwszego miejsca zerowego (x=2) które jest parzyste, więc 'odbijamy (wąż
zostaje po 'dolnej' czyli 'ujemnej' stronie)
6) dociągamy do drugiego miejsca zerowego (x=1), które także jest parzystego stopnia, więc
'odbijamy'
7) 'dociągamy' do kolejnego miejsca zerowego (x=0), które jest nieparzystego stopnie, więc
'przechodzimy' przez oś na część górną (dodatnią)
8) dociągamy do kolejnego miejsca zerowego (x=−2), które jest nieparzystego stopnia, więc
'przechodzimy' przez oś
9) nie ma więcej miejsc zerowych, więc 'puszczamy węża' w nieskończoność
4) rysowanie zaczynam od góry JEŻELI a>0 ; a od doły JEŻELI a<0 (w naszym przypadku będzie od
dołu bo a = −3 <0)
5) 'dociągamy' do pierwszego miejsca zerowego (x=2) które jest parzyste, więc 'odbijamy (wąż
zostaje po 'dolnej' czyli 'ujemnej' stronie)
6) dociągamy do drugiego miejsca zerowego (x=1), które także jest parzystego stopnia, więc
'odbijamy'
7) 'dociągamy' do kolejnego miejsca zerowego (x=0), które jest nieparzystego stopnie, więc
'przechodzimy' przez oś na część górną (dodatnią)
8) dociągamy do kolejnego miejsca zerowego (x=−2), które jest nieparzystego stopnia, więc
'przechodzimy' przez oś
9) nie ma więcej miejsc zerowych, więc 'puszczamy węża' w nieskończoność