` Artur: Uzupełnić symbolami <,>,=. Napisać uzasadnienie bez rachunków. 3 ∫(x−1)⁵ 0 Niestety nie mam pojęcia jak się to zrobić bez policzenia całki, a narysować bez programu nie umiem, ktoś ma jakiś pomysł ?

kochanus_niepospolitus: ale gdzie tutaj masz wstawić znaki równości bądź nierówności?

Artur: Powinno być 3 ∫(x−1)⁵dx ....0, bo.... 0

kochanus_niepospolitus: >0 , bo 1) Wynikiem całki oznaczonej jest pole powierzchni figury pomiędzy funkcją podcałkową a osią OX. 2) Funkcja (x−1)⁵ jest funkcją rosnącą i 'nieparzystą względem x=1' (szczerze mówiąc, to nie mam pojęcia czy to jest 'poprawne matematycznie' określenie). 3) Granica całkowania nie jest 'symetryczna względem x=1. Bądź inaczej: 1) Wynikiem całki oznaczonej jest pole powierzchni figury pomiędzy funkcją podcałkową a osią OX 2) Funkcja (x−1)⁵ jest funkcją 'nieparzystą względem x=1' (szczerze mówiąc, to nie mam pojęcia czy to jest 'poprawne matematycznie' określenie). Z czego wynika, że ∫₀² (x−1)⁵ = 0 3) Funkcja (x−1)⁵ jest rosnąca (i z punktu (2)), więc całka ∫₀³ (x−1)⁵ = ∫₂³(x−1)⁵ > 0

piotr1973:

Artur: Wszystko fajnie, tylko ja nie mogę tego udowodnić, po przez obliczenie całki, bez rachunków(Liczenie całki)

Artur: Bardziej mnie ciekawi fakt, jak narysować taka funkcję bez uzywania programu do rysowania wykresów.

kochanus_niepospolitus: Artur ... a gdzie ja tutaj dokonałem rachunków ?

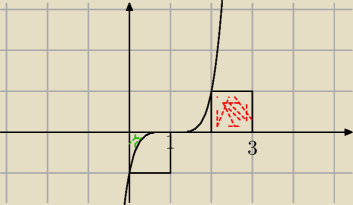
piotr1973: pole zielone jest mniejsze o czerwonego czyli ∫>0

kochanus_niepospolitus: a co za problem narysować (schemat) takiego wykresu? 1) Postać funkcji f(x) = x^2α+1 dla α∊N₊ powinieneś znać na pamięć (a jak nie to do książek). 2) Miejsce zerowe zerowe jesteś w stanie szybko wyznaczyć −−− x=1 3) a=1, więc dla x=0 i x=2 wartość funkcji będzie wynosi −1 i 1 ( f(0) = −1 i f(2) = 1) 4) obliczasz sobie f(3) = 2⁵ i już masz wszystko co jest Ci potrzebne do wykonania szkicu wykresu f(x) = (x−1)⁵

kochanus_niepospolitus: Jednak to zadanie NIE POLEGA na tym, abyś z rysunku 'na oko' zobaczył które pole będzie większe ... tylko abyś zauważył że część 'pól' się 'znosi' i zostaje tylko kawałeczek funkcji, gdzie jest ona dodatnia (więc i wartość całki będzie dodatnia)

Artur: Ok, dzięki.