Liczby zespolone: postać trygonometryczna. Alky: Liczby zespolone: postać trygonometryczna. Niech α będzie miarą kąta łukowego, którego sinus jest równy 3/5. Zapisz w postaci trygonowetrycznej 3+4i. do postaci trygonowmetrycznej brakuje mi tylko α, bo wiem ze cos α=4/5 ( z jedynki trygonometrycznej ) a sin α=3/5, ale nie wiem jak na tej podstawie znalesc kąt. Pomocy

Mila: A po co chcesz to zrobić, raczej nie dasz rady podać dokładnego kąta.

	4
φ=arctg(		) i to będzie wartość przybliżona, gdy odczytasz.
	3

Alky: Ale żeby podać liczbę zespoloną z ( 3+4i ) w postaci trygonowmtrycznej z=r(cos α +i*sinα) , gdzie r ot moduł z muszę miec chyba α, nie jest tak ?

Alky: A jeżeli nie, to masz jakiś pomysł, bądź mógłabyś mnie nakierować, co dalej z tym zadaniem ?

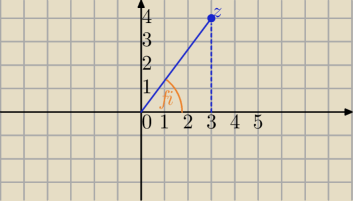
Mila: Jeżeli masz polecenie : Przedstaw liczbę z=3+4i w postaci trygonometrycznej to możesz zapisać :

	4		4
z=5*(cos(arctg(		)+i sin(arctg(		))
	3		3

albo z≈5*(cos(53.13^o)+i sin(53.13^o)) Jeżeli to jest potrzebne do innych rachunków, to warto wiedzieć, że (3+4i)=(2+i)² Przydaje się w równaniach.

Alky: Rozumiem, jednak funkcje cyklometryczne wykraczają poza zakres materiału. Wiem, że można to zapisać w postaci z≈5*(cos(53.13o)+i sin(53.13o)), choć myslalem że muszę to doprowadzić do postaci z π z pomocą znajomości radianów, gdyż tak wyglądały wszystkie pozostałe przykłady. Może masz rację, ale myslalem ze odczytanie z tablic sin/cos będzie zbyt proste, ale jak mówię może o to chodziło. No ot dzieki za pomoc. W sumie to troche dziwne bo całe 2 zad z http://prac.im.pwr.wroc.pl/~kwasnicki/pl/teaching/t/lista-2.pdf bedzie wyglądało bardzo podobnie, ale jeszcze sobie pomysle czy nie da sie tego jakoś doprowadzić do ładnej postaci. W kazdym razie bardzo Ci dziękuję. Pomogłaś

Mila: Godzio tu spojrzy, to doradzi.

Godzio: Trochę mało aktualne, ale .... skoro jest podany kąt α to z jego pomocą trzeba to zapisać

	3		4		π		π
3 + 4i = 5(		+		i) = 5(sinα + icosα) = 5(cos(		− α) + isin(		− α))
	5		5		2		2

No i mamy postać trygonometryczną