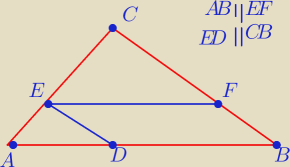
Pomocy.. Robc: Cześć ktoś pomógłby ? Pole trójkąta EFC jest równe 12, a pole ADE jest równe 3. Oblicz pole trójkąta ABC

Eta: 30

Robc: odpowiedzi: 27, 15, 36, 24

ax: pobaw się skalami podobieństwa

ax: 27

Robc: a możesz jakoś jaśniej ?

Robc: chciałbym umieć rozwiązać, nie chcę strzelać /

ax: jak zauważysz, że wysokość trójkąta ABC jest trzy razy większa od wysokości trójkąta ADE (a są to trójkąty podobne) ... to będziesz w domu

ax: wiesz dlaczego skala podobieństwa ΔEFC i ΔADE k=2

Robc: Założyłeś że te dwa trójkąty są podobne i zastosowałem wzór Δ/Δ= k² k=2 no ale że wysokość 3 razy większa to nie widzę ./...

ax: skoro wysokość trójkąta ADE=1n wysokość trójkąta EFC=2n to wysokość trójkąta ABC=3n

ax: znasz skalę podobieństwa ... znasz pola

Robc: i taak nie wiem co dalej ....

ax: Chłopie ... te wszystkie trzy trójkąty są podobne Między najmniejszym i średnim skalę znasz Skoro na wysokość największego składają się wysokości małego i średniego to znasz skalę miedzy największym i najmniejszym

Robc: wysokość dużego 3n, to znaczy ze skala to 3 ? ale co dalej z tym ? ...

Robc: czy skala pomiędzy najwiekszym a najmniejszym √3 ?

ax: skoro największy i najmniejszy to skala 3 ... to pole największego 9 razy większe od pola najmniejszego

Jack:

	ah
Pmałego =		= 3
	2

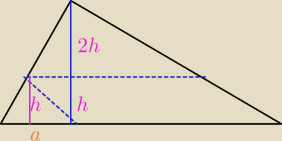
P_całego = k² * P_małego

	3h
k =		= 3 −−−>>. k2 = 9
	h

więc P_całego = 9 * P_małego = 27

Robc: no dobra coś tam już rozumiem mniej więcej... nie zawracam juz głowy

Robc: no dobra to jeszcze tylko czemu ... k² jest ? i dopiero potem razy 3

Robc: doobra wiem dziękiwas

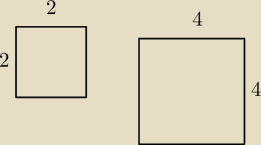
Jack: masz dwa kwadraty

	4
sa one podobne w skali −> duzy do malego −>> k =		= 2
	2

pole malego = 2*2 = 4 pole duzego = 4*4 = 16

pole duzego		16
	=		= 4
pole malego		4

pola sa podobne w skali k², boki w skali k objetosc jako 3wymiarowa by byla podobna w skali k³

Mila: 1) stosunek pól figur podobnych jest równy kwadratowi skali podobieństwa⇔

PΔEFC		12		H
	=		=(		)2⇔
PADE		3		h

3H²=12h² H²=4h² H=2h 2) ΔEFC∼ΔABC: h_ΔABC=3h

12		2h
	=(		)2
P		3h

P=27 ==========