Podaj równanie stycznej do krzywej w punkcie i sporządź rysunek Krzysiek: x² + 4y² − 2x − 3 = 0 P(1, −1)

PW: (x − 1)² + 4y² = 4

(x − 1)2		y2
	+		= 1
4		1

i tak z lenistwa przesunąłbym to razem z punktem P w lewo o 1.

Mila:

(x−1)2		y2
	+		=1 elipsa
22		1

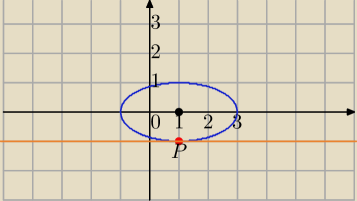
S=(1,0) a=2,b=1 F(x,y)=x² + 4y² − 2x − 3 s: y=−1 P=(1,−1) − punkt stczności Z wzorów:

	dF		dF
s:		(x0)*(x−x0)+		(y0)*(y−y0)=0
	dx		dy

dF		dF
	=2x−2 ,		(1)=2−2=0
dx		dx

dF		dF
	=8y,		(−1)=−8
dy		dy

s: 0*(x−1)+(−8)*(y+1)=0 −8*(y+1)=0 s: y+1=0

PW: Mila, chyba "zbyt mądrze" rozwiązałaś to zadanie. Trzeba było "podać równanie" − zobaczyć, że to elipsa, a potem jako oczywiste podać równanie stycznej w tym punkcie.

Krzysiek: Dziękuję