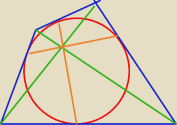
Dowód, punkty styczności, przekątne Rafal44: W czworokącie wypukłym ABCD punkty K, L, M i N są punktami styczności okręgu wpisanego w ten czworokąt kolejno z bokami AB, BC, CD i DA. Wykaż, że punkt przecięcia przekątnych AC i BD pokrywa się z punktem przecięcia prostych KM i LN.

anaisy: Niech X=CD∩AB, Y=AD∩BC, S=LM∩KN, R=MN∩LK. Wtedy z twierdzenia Pascala dla sześciokąta MNKKLM mamy, że X leży na prostej SR. Analogicznie możemy pokazać, że Y leży na prostej SR. Niech E=MK∩NL. Punkt E leży na biegunowej X i na biegunowej Y wrt (MLKN), zatem z twierdzenia 1.11 (http://students.mimuw.edu.pl/~tc319421/dwustosunek.pdf) XY jest biegunową E wrt (MLKN). Z zadania 2.1 mamy, że SE jest biegunową R wrt (MLKN). Ponadto R leży na biegunowej D i biegunowej B wrt (MLKN), czyli B i D leżą na SE. Analogicznie pokazujemy, że A i C leżą na RE.