całka oznaczona
miś: Polecenie: oblicz całkę oznaczoną:
π
∫ x2 sinx dx
−π
8 lut 22:06
ICSP: funkcja podcałkowa jest nieparzysta, więc całka po przedziale symetrycznym jest równa 0.
8 lut 22:10
52: ICSP na pewno nie studiujesz matematyki

?
8 lut 22:19
ICSP: tajemnica

8 lut 22:20
miś: a można jaśniej?
8 lut 22:37
yyhy: Jeżeli f(x)=f(−x) to ∫−aa f(x)=0
8 lut 22:40
yyhy: Jeżeli f(x)=−f(x) ***
8 lut 22:41
yyhy: Sorry... f(−x)=−f(x) ***
8 lut 22:41
yyhy: 

Juz jest ok, chciałm szybko napsiać bo spadam
8 lut 22:41
ICSP: Jeśtli
f(x) = −f(−x)
to
−a∫a f(x) dx = 0
8 lut 22:43
Jerzy:
Pokażcie mu jak to policzyç, a nie znęcajcie siè

8 lut 22:45
8 lut 22:49
miś: dzięki!
8 lut 22:55
Mila:
∫x
2*sinx dx=..
[x
2=u, 2xdx=du , dv=sinx dx, v=∫sinx dx=−cosx]
=−x
2*cosx+2∫xcosx dx= jeszcze raz przez części:
[x=u, dx=du, dv=cosx dx, v=sinx]
cd
−x
2cosx+2*[xsinx −∫sinx dx]=
=−x
2*cosx+2xsinx +2cosx
−π∫
πx
2*sinx dx=−π
2*cosπ+2π*sinπ+2cosπ−[−π
2*cos(−π)−π*sin(−π)+2cos(−π)=
=−π
2+0−2+π
2−0+2=0
Tak jak napisał
ICSP.
Wyjaśnienie:
f(x)=x
2*sinx
f(−x)=x
2*sin(−x)=−x
2*sinx ⇔ funkcja nieparzysta
Wykres jest symetryczny względem (0,0).
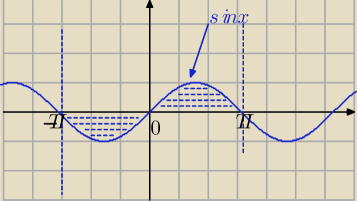
Popatrz jak jest w przypadku y=sinx,
−π∫
πsinx dx=0
tak samo będzie dla f(x)=x
2sinx
8 lut 23:09
 ?
?


 Juz jest ok, chciałm szybko napsiać bo spadam
Juz jest ok, chciałm szybko napsiać bo spadam

 ∫x2*sinx dx=..
[x2=u, 2xdx=du , dv=sinx dx, v=∫sinx dx=−cosx]
=−x2*cosx+2∫xcosx dx= jeszcze raz przez części:
[x=u, dx=du, dv=cosx dx, v=sinx]
cd
−x2cosx+2*[xsinx −∫sinx dx]=
=−x2*cosx+2xsinx +2cosx
−π∫πx2*sinx dx=−π2*cosπ+2π*sinπ+2cosπ−[−π2*cos(−π)−π*sin(−π)+2cos(−π)=
=−π2+0−2+π2−0+2=0
Tak jak napisał ICSP.
Wyjaśnienie:
f(x)=x2*sinx
f(−x)=x2*sin(−x)=−x2*sinx ⇔ funkcja nieparzysta
Wykres jest symetryczny względem (0,0).
Popatrz jak jest w przypadku y=sinx,
−π∫πsinx dx=0
tak samo będzie dla f(x)=x2sinx
∫x2*sinx dx=..
[x2=u, 2xdx=du , dv=sinx dx, v=∫sinx dx=−cosx]
=−x2*cosx+2∫xcosx dx= jeszcze raz przez części:
[x=u, dx=du, dv=cosx dx, v=sinx]
cd
−x2cosx+2*[xsinx −∫sinx dx]=
=−x2*cosx+2xsinx +2cosx
−π∫πx2*sinx dx=−π2*cosπ+2π*sinπ+2cosπ−[−π2*cos(−π)−π*sin(−π)+2cos(−π)=
=−π2+0−2+π2−0+2=0
Tak jak napisał ICSP.
Wyjaśnienie:
f(x)=x2*sinx
f(−x)=x2*sin(−x)=−x2*sinx ⇔ funkcja nieparzysta
Wykres jest symetryczny względem (0,0).
Popatrz jak jest w przypadku y=sinx,
−π∫πsinx dx=0
tak samo będzie dla f(x)=x2sinx