GEOMETRIA ANALITYCZNA justynka: Prosta k o równaniu y=ax+b, gdzie a∊(0;1), przechodząca przez punkt P(−3;2) przecina dodatnią półoś osi OY w punkcie A i ujemną półoś osi OX w punkcie B. Pole trójkąta OAB, gdzie O(0;0) jest równe 12,5. a) Wyznacz równanie kierunkowe prostej k. b) Prosta m, która jest obrazem prostej k w jednokładności o środku O(0;0) i skali k=6, przecina oś OY w punkcie D, zaś OX w punkcie C. Oblicz pole trapezu ABCD.

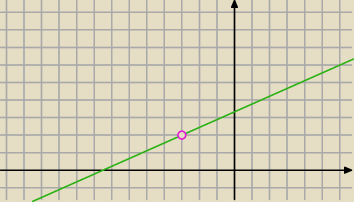
===: a) y−2=a(x+3) ⇒ y=ax+3a+2 Oy przecina w 3a+2

	−3a−2
Ox
	a

(3a+2)2
	=12,5
2a

9a²−13a+4=0 Δ=169−144=25 a₁=1 nie spełnia warunków zadania a₂=4/9

	4		1
zatem szukana prosta to y=		x+3
	9		3