` Artur: Dziedzina: (4−2x²)(y²−10)≥0 Po wymnożeniu: 4y²−64−2x²y²+32x²≥0 Myślałem nad nierównością koła, ale jest to nieszczęsne 2x²y²

Artur: zamiast −10 powinno być −16*

kochanus_niepospolitus: krok 1: NIE WYMNAŻAJ krok 2: pomyśl −−− masz wyznaczyć dziedzinę, a nie rysować: krok 3: jeżeli y∊(−√10 ; √10) to x MUSI ∊(−∞;−√2>∪<√2;+∞) krok 4: a jeżeli (y²−10) jest dodatnie, to co wtedy nam to mówi odnośnie 'y' i 'x' ?

kochanus_niepospolitus: krok 5: paradoksalnie −−− w tym momencie możesz 'spróbować' to narysować

Artur: Niestety polecenie to naszkicować dziedzinę

kochanus_niepospolitus: i zobaczysz, że jest to 'krzyż bez środka'

Artur: Także, niestety ale jestem zmuszony, jakoś to rozwiązać.

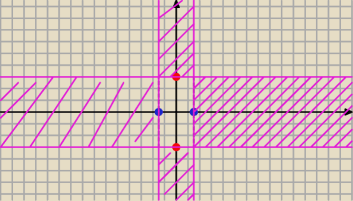
kochanus_niepospolitus: (pod koniec już nie chciało mi się 'kreskować' )

kochanus_niepospolitus: jeszcze raz Ci piszę −−− NIE WYMNAŻAJ z tej postaci która masz ŁATWIEJ będzie Ci ten krzyż narysować

Artur: O kurde, dzięki teraz tylko moje pytanie, w jaki sposób to wyznaczyłeś ?

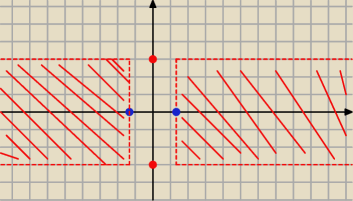
kochanus_niepospolitus: jak już pisałem: jeżeli y∊(−√10; √10) to x∊(−∞;−√2)∪(√2;+∞) więc mamy (patrz rysunek kropki oznaczają: √10 i √2) −−−− zauważ, ze 'linie są przerywane' (patrz przedziały) następnie robisz przedział: y = −√10 lub y = √10 to x∊ R a na koniec robisz y∊ (−∞; −√10)∪(√10; +∞) to (uwaga) x∊<−√2 ; √2>

kochanus_niepospolitus: i w efekcie powstaje Ci to co narysowałem

kochanus_niepospolitus: poprawka do pierwszego + rysunek: powinno być: y∊(−√10; √10) to x∊(−∞;−√2>∪<√2;+∞) i te dwie linie nie powinny być już na tym rysunku przerywane

kochanus_niepospolitus: no i nie powinno być +/− √10 tylko +/−p{16 = +/− 4 (bo pomyliłeś się na początku piszą ... ale samo rozumowanie pozostaje niezmienione).

Artur: Dzięki wielkie, już teraz wiem o co chodzi !

Artur: W przypadku dziedziny ln(x²+1) to po prostu x²+1>0 Czyli parabola przesunięta o 1 wartość w górę ?

kochanus_niepospolitus: dziedziną funkcji y(x) = ln(x²+1) będzie D_f = R

Artur: No tak, ale z definicji logarytmu, a>0 czyli x²+1>0 ?

kochanus_niepospolitus: nom ... czyli x²>−1 ... czyli x∊R

Artur: no fakt