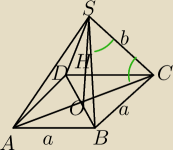
 W ostrosłupie prawidłowym czworokątnym krawędź podstawy ma długość a. Kąt między krawędzią
boczną i podstawą jest równy kątowi płaskiemu przy wierzchołku ostrosłupa. Oblicz objętość
tego ostrosłupa.
Z tr BCS z tw cosinusów wyznaczyłam cosα=a2−2b2 /(−2b2) (zaznaczony na zielono), z tr
prostokątnego np SBO cosα= (a*√2/2)/H. Porownałam oba cosinusy i wychodzą cuda trudne do
wyliczenia. Ktoś jakiś lepszy pomysł?
W ostrosłupie prawidłowym czworokątnym krawędź podstawy ma długość a. Kąt między krawędzią
boczną i podstawą jest równy kątowi płaskiemu przy wierzchołku ostrosłupa. Oblicz objętość
tego ostrosłupa.
Z tr BCS z tw cosinusów wyznaczyłam cosα=a2−2b2 /(−2b2) (zaznaczony na zielono), z tr
prostokątnego np SBO cosα= (a*√2/2)/H. Porownałam oba cosinusy i wychodzą cuda trudne do
wyliczenia. Ktoś jakiś lepszy pomysł?
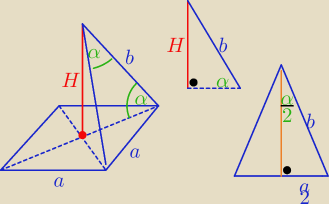
| a | α | α | |||||||||||||
H=b*sinα i b= | , sinα=2sin | *cos | |||||||||||||
| 2 | 2 |
| α | ||||||||||||||||||
⇒ H= | = a*cos | ||||||||||||||||||
| 2 |
| 1 | ||
V= | a2*H= ............ | |
| 3 |
 Mam jednak pytanie, bo w ostatecznym rozwiązaniu zostanie cos α/2, nie będzie
to błędem? bo wydawało mi się, że w wyniku może pozostać tylko a. O kątach było powiedziane
tylko, że są równe, ale nie było nic o mierze. Jak próbowałam rozwiązać to zadanie starałam
sięcały czas wyeliminować funkcje trygonometryczną z wyniki − i własnie to mi nie wychodziło
Mam jednak pytanie, bo w ostatecznym rozwiązaniu zostanie cos α/2, nie będzie
to błędem? bo wydawało mi się, że w wyniku może pozostać tylko a. O kątach było powiedziane
tylko, że są równe, ale nie było nic o mierze. Jak próbowałam rozwiązać to zadanie starałam
sięcały czas wyeliminować funkcje trygonometryczną z wyniki − i własnie to mi nie wychodziło
