Zadanie a w postaci trygonometrycznej zadanie b w postaci Kramera Kamil: Witam, Potrzebuje rozwiazania zadan a) 1+i√3 W postaci trygonometrycznej oraz zadanie b) 3x−5y+3z=1 4x+3y−5z=2 5x−2y+7z=10 W postaci Kramera

5-latek: 2) to wyznaczniki stopnia 3 wiec licz i Cramera

Eta: Widzisz,że takie zadanka już 5−latki ........ liczą

5-latek:

Kamil: a wiesz moze ile bedzie wynosic fi z √8−6i cos wynosi √8 : √2 sin wynosi −√6 : √2 nie wiem jak zrobic mianownik na tej stronie

Mila: Kamil napisz to zadanie, o którym piszesz 20:10.

Kamil: √8−√6i Licze modul |z| = √2 potem licze cos i sin aby wyznaczyc fi cos liczymy wzorem cos fi= a/|z| sin fi = b/|z| I wychodza mi kosmiczne wyniki cos wynosi √8 : √2 sin wynosi −√6 : √2 Nie moge obliczeyc fi Dzieki Mila za zainteresowanie

5-latek: Kamil jeśli chodzi o zespolone to jeszcze nie pomoge .

Mila: 3x−5y+3z=1 4x+3y−5z=2 5x−2y+7z=10 W: 3 −5 3 4 3 −5 5 −2 7 W=229 W_x: 1 −5 3 2 3 −5 10 −2 7

	229
Wx=229⇔x=		=1
	229

W_y: 3 1 3 4 2 −5 5 10 7 W_y=229⇔y=1 W_z: 3 −5 1 4 3 2 5 −2 10 −−−−−−−−−−− W_z=229⇔z=1

5-latek:

	√8		2√2
cos=		=		= 2 (ale cosinus nie może być rowny 2
	√2		√2

	−√6		−√3*√2
sin=		=		=−√3 to samo
	√2		√2

No chyba z etu chodzi o co innego

Mila: z=√8−√6i tak, czy tak: z=√8−6i

Kamil: o dzieki widze ze ktos ogarnia ja najpierw probowalem wyznaczyc w kolumnie 0 1 0 Za duzo kombinowalem

Kamil: 2 opcja u mnie pierwiastek nie wychodzi

Kamil: Mila: z=√8−√6i tak, czy tak: z=√8−6i prawidlowa

Mila: z=√8−6i i masz obliczyć pierwiastki?

Mila: Jeśli masz macierz 3x3 to wyznacznik liczysz metoda Sarrusa.

Kamil: musze obliczy funkcje trygonometryczna. nie wychodza mi niestety potegi na tej srtonie

Mila: |8−6i|=√8²+6²=10

	4
cosφ=
	5

	3
sinφ=
	5

nie wyznaczysz dokładnie kąta, aby przedstawić liczbę (8−6i) w postaci trygonometrycznej Przepisz dokładnie z książki treść zadania. Pierwiastki możesz obliczyc inaczej: √8−6i=(x+iy)⇔ (x+iy)²=8−6i x²+2xyi−y²=8−6i x²−y²=8 2xy=−6 x²+y²=10 2x²=18 x²=9 x=3 lub x=−3 x*y=−3 3*y=−3 lub −3*y=−3 y=−1 lub y=1 z₀=3−i z₁=−3+i

Kamil: ok dzieki

Kamil: dzieki za pomoc

Mila: O to chodziło?

Kamil: masz racje nie mozeliwosci wyciagnac fi z tych liczb wiec trzeba obliczyc inna metoda

Mila: Na drugi raz pisz dokładnie treść zadania.

Kamil: a w tej metodzie cramera 3 −5 3 4 3 −5 5 −2 7 W=229 to mnozlylismy metoda na krzyz. Mozesz mi tylko ten jeden przyklad rozpisac. Reszte sobie potem rozpisze.

PW: Metody na krzyż n i e m i e l i ś m y. Możesz nas oświecić?

Kamil: Juz wiem o co chodzi widzialem ze Mila wie o co chodzi dlatego pytalem i jeszcze raz dzieki za pomoc Trzymajcie sie

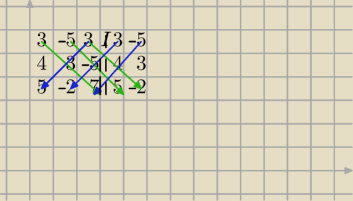
Mila: 3 −5 3||3 −5 4 3 −5||4 3 5 −2 7||5 −2 W=3*3*7+(−5)*(−5)*5+3*4*(−2)−[3*3*5+3*(−5)*(−2)+(−5)*4*7)= =63+125−24−(45+30−140)= =164−75+140=229

PW: A, to mieliśmy, tyle że nazywało się metodą Sarrusa w czasach mniej pobożnych.