Egzamin Architekt: Jak narysować wykres takiej funkcji y=√|2−|x−1|

5-latek: cos brakuje

Architekt: y=√|2−|x−1||

5-latek: ja osobiście bym zrobil tak 1. Wyznaczyl dziedzine czyli |2−|x−1||≥0 2. Potem bym wzial kilka argumentow z dziedziny i wyznaczyl dla nich wartosci funkcji y 3. Naniosl to na papier milimetrowy i sporzadzil przybliżony wykres

Jerzy: Ja bym rysował w przedziałach

ikd: y=√||x−1|−2} Startujesz z √x, nakładasz wartość bezwzględną na x, przesuwasz o wektor [2,0], znowu nakładasz | | na x i przesuwasz o wektor [1,0].

5-latek: J Możesz pokazc jak ? Powiem szczerze sam tez skorzytam

ikd: Po prostu wykonujesz kolejne przekształcenia wykresów funkcji, np nałożenie | | na x powoduje odbicie symetryczne części wykresu dla x≥0 względem osi OY.

piotr: −(−x−1)^1/2 x<=−1 (x+1)^1/2 −1<x≤ 1 −(3−x)^1/2 1<x<=3 (x−3)^1/2 x>3

Architekt: Nadal nie bardzo wiem jak

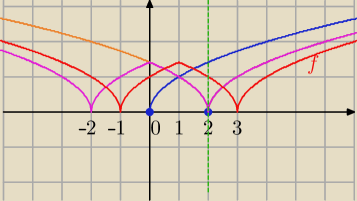
Mila: f(x)=√|(|x−1|−2)| 1)y=√x→T_[2,0]⇒ 2) y= √x−2→S_x=2⇒ 3) y=√|x−2| →S_OY tej części wykresu, która leży po prawej stronie OY, tę z lewej pomijamy⇒ 4) y=√|(|x|−2)|→T_[1,0]⇒ 5) f(x)=√|(|x−1|−2)|