dowód matematyczny duo: zad.1 Z punktu A poprowadzono styczne AQ i AP do okręgu. Przez punkt R a okręgu poprowadzono styczną styczną do okręgu przecinającą prost AQ i AP w punktach B i C. Wiedząc, że AP= a, uzasadnij, że obwód trójkąta ABC jest równy 2a. zad.2 Uzasadni, że jeśli liczby rzeczywiste a,b,c spełniają warunek a<b<c, to b+c/2>a+b+c/3. Bardzo proszę może ktoś zechce pomóc? Będę wdzięczna.

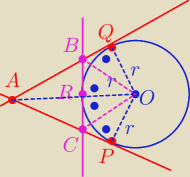
Janek191: I AP I = a = I AQ I Mamy I CP I = I CR I oraz I BQ I = I BR I więc I AC I + I CR I = a oraz I AB I + I BR I = a Obwód Δ ABC = 2 a ===============

duo: Dziękuję Janku. Jestem Ci niezmiernie wdzięczna.