Oblicz pole figury zawartej między liniami 4-x^2=3x Magda: Oblicz pole figury zawartej miedzy liniami 4−x²=3x

bezendu: Nie wiem o jakie linie chodzi

Magda: y1 = 4−x² , y2=3x. Sorki, mój błąd

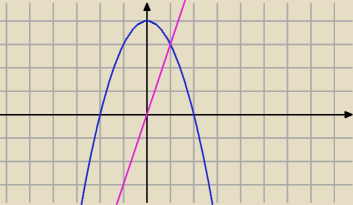
bezendu: P=[∫(f(x)−g(x)]dx w granicach całkowania x∊(ustal sobie) f(x)−funkcja która ogranicza od góry g(x)−funkcja która ogranicza od dołu wylicz miejsca przecięcia f(x)=g(x) to będzie przedział całkowania jeden punkt już masz x∊[? ,1]

Magda: wiem jak to obliczyć. Chciałam po prostu sprawdzić czy wynik się zgadza

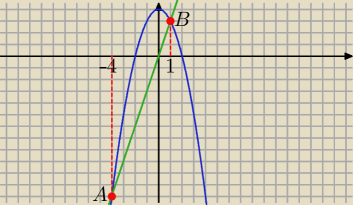
Mila: Punty przecięcia: (−4,−12) , (1,3)

	125
P=−4∫1(4−x2−3x) dx=
	6

bezendu: Nie podałaś wyniku więc nikt nie wiedział, że interesuję Ci tylko wynik a nie jak zrobić zadanie. Przepraszam jasnowidzem jeszcze nie jestem