Zespolone Benny:

	i−1
z3=
	2

Jest jakiś sposób na szybkie rozwiązywanie takich równań czy klasycznie?

	φ+2kπ		φ+2kπ
w0=3√|z|*(cos		+isin		)
	3		3

Janek191:

	1		1
z3 = −		+		i
	2		2

i wzór w_k = ... , gdzie k = 0,1,2

Benny: I drugie zadanko: z' to sprzężenie

	1−z'		π
arg(		)=
	1+z'		2

Wynika z tego, że część rzeczywista ma być równa 0, a urojona ≥0.

	1−x2−y2+2iy		π
Po przekształceniach mam arg(		)=		, x≠−1 i y≠0.
	(1+x)2+y2		2

Mam więc: y>0 i x∊(−1, 1> Też da się to inaczej rozwiązać?

Benny: @Janek191, więc szybciej się nie da lub inaczej?

PW:

	π
Jeżeli argument pewnej liczby jest równy		, to chyba tą liczbą jest i,
	2

czyli

	1 − z̅
		= i
	1 + z̅

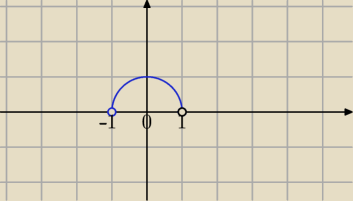
Benny: Kurczę nie napisałem całej treści. Na płaszczyźnie zespolonej narysować zbiór:

	1−z̅		π
A={z∊ℂ: arg(		)=		}.
	1+z̅		2

Benny: x∊(−1; 1> i y∊(0; 1>

piotr: (1−x+yi)/(1+x−yi)=i

PW:

	π
Dobrze że napisałem "chyba" Argument		mają wszystkie liczby na dodatniej półosi
	2

urojonej, a więc mające postać ki, k∊(1,∞).

Benny:

	1
Oj, PW myślę, że mam racje. Co jeśli z=		i?
	2

Benny: Chociaż masz tak jak ja tylko pewnie miało być k∊(0; +∞)

piotr: ((1−x)²+y²)/((1+x)²+y²)=1 ⇒ x=0 atan(−y/(1−x))−atan(−y/(1+x))=pi/2 ⇒ y∊∅ nie ma rozwiązania

piotr: mój post z 19:02 błędny

piotr:

	1+i y		π
((1−x)2+y2)/((1+x)2+y2)=1 ⇒ x=0 ⇒arg		=		⇒y=1⇒ z=1
	1−i y		2

Mila: Liczba :

	1−x2−y2+2yi
w=		jest liczbą czysto urojoną oraz Im(w)>0⇔
	1+2x+x2+y2

	1−x2−y2
Re(w)=		=0⇔x2+y2=1 ∧ x≠−1 ∧ y≠0⇔(*) x∊(−1,1> i y∊<−1,1>\{0}
	1+2x+x2+y2

i

	2y		2y
Im(w)=		=		>0⇔
	1+2x+x2+y2		2x+2

y>0 i 2x+2>0⇔ y>0 i x>−1 i (*) lub y<0 i x<−1 − sprzeczność z warunkiem (*) ======================== Zatem x∊(−1,1) i y∊(0,1> Nie wiem, czy to wszystko.

Benny: Milu skąd w mianowniku wzięło się 2x+2 oraz czemu wyrzuciłaś x=1. Rozumiem, że moje ostatnie rozwiązanie jest dobrze?

Mila: Mianownik: 1+2x+x²+y²=1+2x+1=2+2x Punkt (1,0) nie należy do dziedziny bo y=0 i wtedy Im(w)=0 a masz warunek Im(w)>0 Oblicz:

(1,0)−(1,0)
	=0
(1,0)+(1,0)

Benny: Och racja, nawet o tym nie pomyślałem. Dziękuje