Kąt nachylenia przekroju do płaszczyzny podstawy.
agatka: W ostrosłupie prawidłowym trójkątnym poprowadzono przekrój płaszczyzną zawierającą krawędź
podstawy i prostopadłą do przeciwległej krawędzi bocznej. Wiedząc,że kąt między sąsiednimi
krawędziami ma 2α oblicz
a)cosinusβ przy wierzchołku przekroju należącym do krawędzi bocznej.
b) cosinus kąta nachylenia przekroju do płaszczyzny podstawy.
Proszę o wskazówki i rysunek. Z góry dziękuję.
5 lut 10:25
agatka: Zerknijcie na to zadanie, proszę.
5 lut 16:54
Janek191:
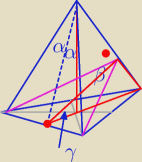
5 lut 17:35
Mila:
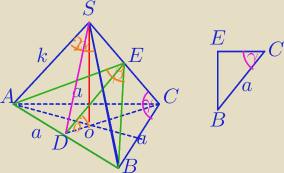
Podpowiedź.
DE⊥SC
γ=90
o−α
W ΔBEC:
|EB|=a*cosα
|EC|=a*sinα
Próbuj dalej sama.
5 lut 17:45
Kacper:
biorę

5 lut 18:25
agatka: Mila, na jakiej podstawie twierdzisz,że trójkąt BCE jest prostokątny?
Wiem,że ΔDCE jest prostokątny.
5 lut 22:41
Mila:
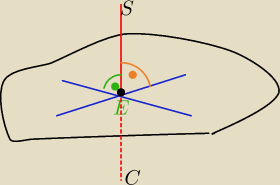
Prosta SC jest prostopadła do płaszczyzny ABE i przebija ją w punkcie E,
to jest prostopadła do każdej prostej leżącej
w tej płaszczyźnie przechodzącej przez punkt przebicia.
5 lut 22:59
agatka: Dziękuję Ci bardzo, pewnie,że tak.
Jak mogłam o tym zapomnieć.
6 lut 08:18

 Podpowiedź.
DE⊥SC
γ=90o−α
W ΔBEC:
Podpowiedź.
DE⊥SC
γ=90o−α
W ΔBEC:

 Prosta SC jest prostopadła do płaszczyzny ABE i przebija ją w punkcie E,
to jest prostopadła do każdej prostej leżącej
w tej płaszczyźnie przechodzącej przez punkt przebicia.
Prosta SC jest prostopadła do płaszczyzny ABE i przebija ją w punkcie E,
to jest prostopadła do każdej prostej leżącej
w tej płaszczyźnie przechodzącej przez punkt przebicia.