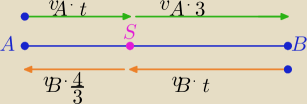HELP Robc: Z miejscowości A i B oddalonych od siebie o 300 km, wyjechały dwa samochody naprzeciw siebie. Pierwszy dotarł do miasta B po 3 h od momentu kiedy minęły się, natomiast drugi dotarł do miasta A po 1 h i 20 minutach od tego momentu kiedy się minęły . Jakie były średnie prędkości samochodów. Ktoś wytłumaczy mi krok po kroku jak robić takiego typu zadanka ?

kochanus_niepospolitus: De facto − mamy w tym zadaniu 3 niewiadome, wiec wystarczy ułożyć 3 równania, aby to rozwiązać. Dane: d = 300 km Szukane: v_A−B = ? v_B−A = ? t₁ = ? <−−− t₁ −−− czas potrzebny kierowcom do dojechania 'punktu mijania się' I teraz równania: 1) Kierowca 'z A do B' przejechał cały dystans (300km) w czasie (t₁ + 3h), więc: v_A−B*(t₁ + 3h) = 300 km 2) Analogicznie z kierowcą 'z B do A': v_B−A*(t₁ + 1h20min) = 300 km 3) suma dróg jaką przebyli obaj kierowcy w czasie t₁ (do czasu mijanki) to także nic innego jak cała odległość pomiędzy miastami (300km), więc: v_A−B*t₁ + v_B−A*t₁ = 300 km −> (v_A−B + v_B−A)t₁ = 300 km No i masz 3 równania i 3 niewiadome .... rozwiązujesz

Eta:

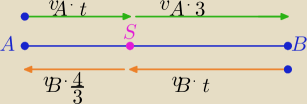
	4
|AB|=300km 1h 20 min=		h i t>0
	3

	4		VA		4
vA*t=vB*		⇒		=
	3		vB		3t

	vA		t
vA*3=vB*t ⇒		=
	vB		3

	4		t
to		=		⇒ t=2 h
	3t		3

v_A*(2+3)=300 ⇒ v_A= 60km/h

	4
vB*(2+		)=300 ⇒ vB= 90km/h
	3

Miejsce spotkania S znajduje się w odległości s=v_A*2= 120 km od miasta A i 180 km d miasta B ( s= v_B*2= 180km)