Narysować zbiór. Lim: {z ∊ C : Im (z³) ≤ 0 } Ktoś mógłby mi wytłumaczyć jak to zrobić za pomocą de Moivre'a. Znalazłem takie zadanie na forum, jednak mi to nie pomogło. Proszę więc o pomoc.

Lim: Jakaś podpowiedź?

Mila: z=x+iy, x,y∊R (x+iy)³=x³+3x²*iy+3*x*i²y²+y³*i³= =x³+3x²y*i−3xy²−iy³= =(x³−3xy²)+(3x²y−y³)*i (3x²*y−y³)≤0 y*(3x²−y²)≤0⇔ (y≥0 i 3x²−y²≤0) lub y≤0 i 3x²−y²≥0) Po kolei: y≥0 i 3x²≤y²⇔ 3|x|≤|y| y≥0 i y≥√3*|x| lub y≤0 i 3x²≥y² ⇔3|x|≥|y| y≤0 i −y≤√3|x|⇔ y≤0 i y≥−√3|x|

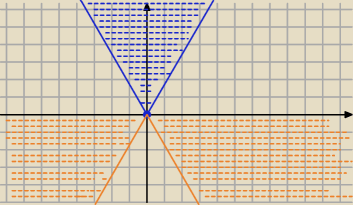
Lim: Może trochę późno pisze, ale czemu zbiór niebieski to y≥√3|x| oraz [P[y≥−√3|x|}]

Lim: y≥−√3|x|} skoro tam jest |y| a potem pojawił się tam minus i 3 nie było pod pierwiastkiem oraz w niebieskim ≤ zmieniło się na ≥?

Mila: No nie bardzo wiem, czy odpowiadać , na ogół tak robię, ale.. dałam tu pytanie 4 lutego i pod Twoim nickiem pojawiło się kilka obrażających mnie komentarzy. Odnośnie Twojego pytania: miało być: lub y≤0 i 3x²≥y² pierwiastkuję obustronnie: √3|x|≥|y| zapomniałam o tym pierwiastku. Ponieważ rozważamy przypadek: y≤0 to |y|=−y Czy to już wyczerpuje wątpliwości?.