Funkcja logarytmiczna
bedor: Sporządź wykres funkcji g(x) = log
2(x+3) +2 i wyznacz współrzędne punktu przecięcia sie
wykresu funkcji g z osią OY.
Funkcję narysowałem ale nie wiem jak wyznaczyć pkt przecięcia, pomoże ktoś?

4 lut 18:26
5-latek:
Jakikolwiek punkt na osi OY ma wspolrzedne (0,y)
4 lut 18:29
Jerzy:
f(0) = log23 + 2
4 lut 18:30
5-latek: Witaj
J 
4 lut 18:31
bedor: no właśnie a jak obliczyć te log23?
4 lut 18:37
Jerzy:
Cześć
małolat 
z tablic, albo kalkulatorem
4 lut 18:38
bedor: czy po prostu log212 wystarczy?
4 lut 18:38
bedor: czy po prostu log212 wystarczy?
4 lut 18:39
5-latek: log
23 jest liczba niewymierna
Możesz ja obliczyć w przybkizeniu
| | log3 | | 0,477 | |
log23= |
| ≈ |
| ≈1,585 |
| | log2 | | 0,301 | |
4 lut 18:42
bedor: dzięki

4 lut 18:47
Mila:
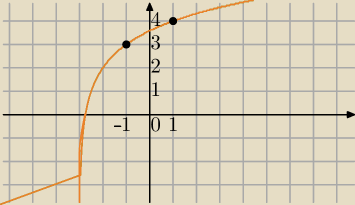
D:
x>−3
Oś Ox:
log
2(x+3) +2=0
log
2(x+3)=−2
2
−2=x+3
x=−2
34 miejsce zerowe f(x)
Oś OY:
x=0 to:
y=log
2(3)+2 i tak podajesz w odpowiedzi.
−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
f(−1)=log
2(−1+3)+2=1+2=3 to wartości dla oszacowania
f(1)=log
2(1+3)+2=2+2=4
3<log
2(3)+2<4
Nie zwracaj uwagi na na tę gałązkę, co skręca na dole, edytor coś fiksuje.
4 lut 18:59

 Jakikolwiek punkt na osi OY ma wspolrzedne (0,y)
Jakikolwiek punkt na osi OY ma wspolrzedne (0,y)

 z tablic, albo kalkulatorem
z tablic, albo kalkulatorem

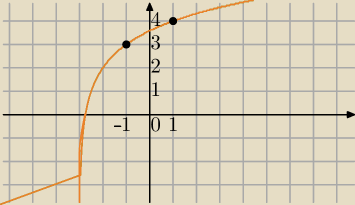 D:
x>−3
Oś Ox:
log2(x+3) +2=0
log2(x+3)=−2
2−2=x+3
D:
x>−3
Oś Ox:
log2(x+3) +2=0
log2(x+3)=−2
2−2=x+3