trapez Adefa: punkty A(−2,−4) B(8,1) C(4,4) są kolejnymi wierzchołkami trapezu rownoramiennego ABCD (nie bedacego rownoleglobokiem) o podstawach AB , CD oblicz rownanie prostej ktora jest osia symetrii tego trapezu oblicz wspl. punktu bedacego srodkiem podstawy CD

5-latek: Odpowiedz sobie najpierw na pytanie Jaki trapez ma os symetrii? Potem zrob rysunek i już pojdzie latwo

Kacper: Swój pomysł?

Adefa: zrobilam , i nic

Adefa: policzylam srodek ab to wyszedl s(3,−1,5)

Kacper: Zrób rysunek.

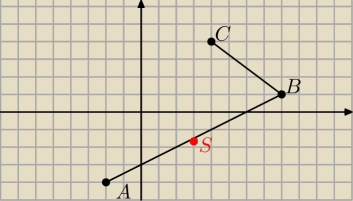
5-latek: Punkt S obliczony dobrze No to os symetrii to przecież prosta prostopadla do AB i przechodzące przez punkt S Napisz to równanie tej prostej

5-latek:

	1
Wspolczynnik kierunkowy a prostej AB=
	2

Wspolczynnik kierunkowy prostej prostopadlej do ABwynosi a₁=−2 Rownanie osi symetrii y=a₁(x−x_s)+y_s y=−2(x−3)−1,5 = −2x+6−1,5= −2x+4,5

5-latek: szkoda ze ucieklas z forum

Adefa: jak policzyc punkt D?

5-latek: Rownanie prostej rownoleglej do AB i przechodzącej przez punkt C y=0,5(x−4)+4= 0,5x−2+4= 0,5x+2 Punkt przecięcia się prostej y=−2x+4,5 i prostej 0,5x+2 będzie srodkiem odcinka CD (oznaczmy go przez P Teraz ze wzoru na wspolrzedne srodka odcinka oblicz wspolrzedne punktu D

Adefa: dzieki za wskazowke