funkcja Heeelp: Wyznacz wszystkie pary (x,y) dla których wielomian P(t)=(t²−4)(t²+yt+x) ma dokładnie dwa miejsca zerowe. Zilustruj ten zbiór na płaszczyźnie. t=2 lub t=−2 więc delta z (t²+yt+x) musi być ujemna więc y²<4x Co teraz? Jak to narysować?

Heeelp: ?

ICSP: Δ < 0 albo drugi nawias jest w jednej z trzech postaci : 1. t² − 4 2. t² + 4t + 4 3. t² − 4t + 4

Heeelp: Nie rozumiem.

Heeelp: Jakby było w takich postaciach co napisałeś/aś to funkcja by miała 4 miejsca zerowe.

ICSP: jakie ?

Heeelp: ok zakumałem xD jak narysować y²<4x (wyszło mi z delty)

ICSP: Zacznij od narysowania y² = 4x.

Heeelp: problem w tym że nie wiem jak to zrobić

Heeelp: narysowac na wykresie dwie funkcje jedna y² druga 4x?

ICSP:

	x2
to narysuj y =		i potem przekręć kartkę o 90o w prawo.
	4

Heeelp: Narysowałem ale nie za bardzo wiem co z tego wykresu wynika. Nie wiem nadal jakie są pary rozwiązań, x ∊(0, ∞) y ∊ R ?

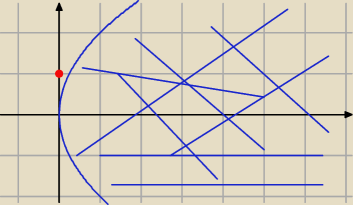
ICSP: y² < 4x (x,y) = (0 , 1) nie spełnia nierówności, więc należy zakreślić obszar po drugiej stronie paraboli. Oczywiście parabola ze względu na słabą nierwónosc powinna byc namalowana przerywaną kreską.

Heeelp: Dzięki