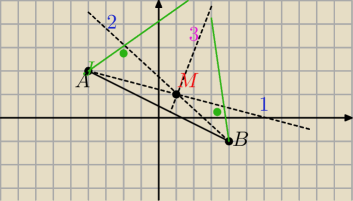
 Jest to szkic rysunku
Wiemy co to jest ortocentrum (punkt przecięcia wysokości trojkata )
Wobec tego możemy napisac równania wysokości nr 1 (czyli prosta przechodzaca przez punkt A i M
)
i równanie wysokości nr 2 (czyli prosta przechodzaca przez punky B i M )
Rownanie wysokości nr 3 to równanie prostej prostopadlej do AB i przechodzącej przez punkt M
Teraz wiemy ze wysokość pada prostopadle na bok wobec tego jeśli napiszemy równanie prostej
prostopadlej do prostej BM i przechodzącej przez punkt A to dostaniemy równanie prostej AC
To samo jeśli napiszemy rownie prostej prostopadlej do prostej AM to dostaniemy równanie
prostej BC
Punkt przecięcia się prostej AC i BC wyznaczy wspolrzedna punktu C
Odleglosc punku C od prostej AB to wysokość nr 3
Majac ta wysokość obliczysz pole tego trojkata
ja bym tak zrobil
Jest to szkic rysunku
Wiemy co to jest ortocentrum (punkt przecięcia wysokości trojkata )
Wobec tego możemy napisac równania wysokości nr 1 (czyli prosta przechodzaca przez punkt A i M
)
i równanie wysokości nr 2 (czyli prosta przechodzaca przez punky B i M )
Rownanie wysokości nr 3 to równanie prostej prostopadlej do AB i przechodzącej przez punkt M
Teraz wiemy ze wysokość pada prostopadle na bok wobec tego jeśli napiszemy równanie prostej
prostopadlej do prostej BM i przechodzącej przez punkt A to dostaniemy równanie prostej AC
To samo jeśli napiszemy rownie prostej prostopadlej do prostej AM to dostaniemy równanie
prostej BC
Punkt przecięcia się prostej AC i BC wyznaczy wspolrzedna punktu C
Odleglosc punku C od prostej AB to wysokość nr 3
Majac ta wysokość obliczysz pole tego trojkata
ja bym tak zrobil
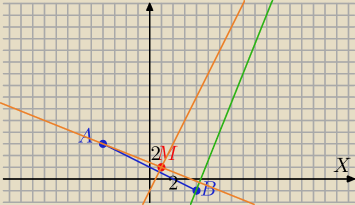 1) Prosta AB:
y=ax+b
A(−4;3), B(4;−1)
3=−4a+b
−1=4a+b
−−−−−−−−−−−−−−+
2=2b⇔b=1 ( co widać na rysunku)
1) Prosta AB:
y=ax+b
A(−4;3), B(4;−1)
3=−4a+b
−1=4a+b
−−−−−−−−−−−−−−+
2=2b⇔b=1 ( co widać na rysunku)
| 1 | ||
3=−4a+1⇔4a=−2⇔a=− | ||
| 2 |
| 1 | ||
AB: y=− | x+1 | |
| 2 |
| 2 | 7 | |||
2=−5a⇔a=− | , i b= | , | ||
| 5 | 5 |
| 2 | 7 | |||
AM: y= − | x+ | , | ||
| 5 | 5 |
| 5 | 5 | |||
y= | x+b i −1= | *4+b⇔b=−11 | ||
| 2 | 2 |
| 5 | ||
y= | x−11 | |
| 2 |
| 5 | |
x−11=2x−1 | |
| 2 |
 Zrobilas to znacznie prościej
Zrobilas to znacznie prościej 

 C(20, 39)
C(20, 39)

 Pozdrawiam
Pozdrawiam