Geometria analityczna
alexaa: Okrąg o: x2+ y2 – 6 √2x + 10 = 0 jest opisany na sześciokącie foremnym ABCDEF.
a) Wyznacz współrzędne wierzchołków sześciokąta, wiedząc, że odcięta punktu A jest
równa √2.
b) Oblicz pole figury F = F1 – F2 , gdzie F1 jest sześciokątem ABCDEF, zaś F2 kołem wpisanym
w ten sześciokąt.
2 lut 17:34
Eta:
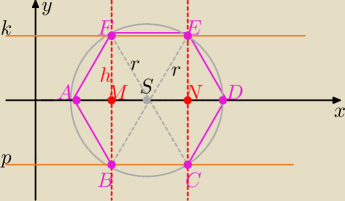
S(3
√2,0) r= |AS|=2
√2 to D(
√2+2r, 0) =(5
√2,0)
| | r√3 | |
proste k i p mają równania y= |h| , h= |
| = √6 |
| | 2 | |
to ; k: y=
√6 i p: y= −
√6
| | 1 | |
M(xA+ |
| r,0) = (2√2.0) , N( 4√2,0) |
| | 2 | |
to B( x
M, y
p)=( 2
√2, −
√6) i C( 4
√2, −
√6)
E( 4
√2,
√6) , F( 2
√2,
√6)
b) a=r to a
2=r
2= 8
| | r2√3 | |
PF1= 6* |
| =.......... = 12√3 |
| | 4 | |
r
w= h=
√6
P
F2= πr
w2= 36π
P
F= .............
2 lut 18:47
siema: ej o co chodzi z tymi kropkami
4 gru 12:02
Eta:
A oto,żeby samemu dokończyć
PF= P(F1)−P(F2)
4 gru 12:22