stereometria przekroje graniastosłupów Archeolog: krawędź podstawy graniastosłupa prawidłowego czworokątnego ma długość a . Przekrój tego graniastosłupa płaszczyzną zawierającą przekątną podstawy i tworzącą z płaszczyzną podstawy kąt dwuścienny o mierze α jest trójkątem. Oblicz pole otrzymanego przekroju. Moje obliczenia: Podstawa tego trójkąta : a√2

	a√2−cos2α
Jest to trójkąt równoramienny i jego boki mają po
	√acosα

(z pitagorasa)

	a*h		a2√2−cos2α
Wtedy pole to P =		, więc P =
	2		2cosα

Wynik w podręczniku jest inny. Dobrze? Źle? Proszę rzucać kamieniami jak zrobiłem głupi błąd i przy okazji go wskazać.

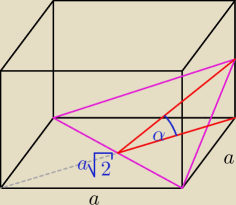
Jack: Hmm... ja bym powiedzial ze to mniej wiecej tak wyglada...

	a√2   2		a√2
wtedy cos α =		=
	h		2h

	a√2
h =
	2cos α

wtedy pole

	a√2   a√2 *   2cos α		a2
P =		=
	2		2cos α

chyba ze zle narysowalem...hmm, ale nie powinno byc zle... moglbys przedstawic tok rozumowania skad boki ?

Mila: Dobrze, Jack.

Kacper: Biorę

23232: δ

23232: emm what a sigma