ostroslup icash: W ostrosłupie prawidłowym trójkątnym tangens kąta nachylenia ściany bocznej do płaszczyzny podstawy jest równy 3√2. Oblicz objętość ostrosłupa, wiedząc, że krawędź podstawy ma długość 6.

	1		36√3
V =		*		* h
	3		4

jak wyznaczyc h?

icash:

GIGANT:

	3√2
tgα =		z treści zadania
	1

	H
tga =		z obliczeń
	√3

H = 3√6 możesz sprawdzić czy dobrze?

icash: Niestety, nie mam jak sprawdzić. A skąd wziąłeś √3 w drugiej linijce?

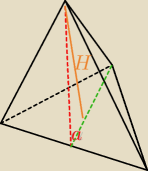GIGANT: No to tak. Narysowałem sobie w podstawie tego ostrosłupa okrąg. Dokładniej mówiąc opisałem okrąg na trójkącie w podstawie ( nie mylić z wpisaniem w trójkąt ! ) Jak z tego dość kiepskiego rysunku widać, wysokość ostrosłupa nie pada dokładnie na środek. ten mniejszy kawałek przerywanego odcinka ( wysokość trójkąta w podstawie ) jest równe 1/3h = r. r to promień okręgu opisanego, a h to wysokość trójkąta w podstawie. Ten dłuższy odcinek to oczywiście 2/3h h możemy obliczyć ze wzoru na wysokość w trójkącie równobocznym bo taki mamy i wyjdzie nam h = 3√3 Potrzebny jest nam krótszy odcinek, który jest równy 1/3h = √3 literka 'a' oznacza tga = 3√3 . Można ułożyć dwa równania tga = 3√3 oraz

	H
tga =
	√3

i teraz przyrównujemy, na krzyż i gotowe.

GIGANT: Ide spac, w razie W jutro tu zerkne, dobranoc

icash: dziękuje

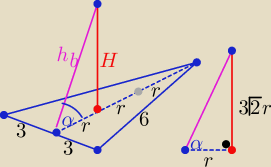Eta: a=6

	a√3
r=		⇒ r=√3 to H= 3√6
	6

V= .............