xsd Anna: z²=i jakie są rozwiązania bo chce sprawdzić czy mam dobrze liczba zespolona to jest

yyhy: (a+bi)²=i a²+2abi−b²=i a²−b²=0 oraz 2ab=1 a=b lub a=−b oraz 2ab=1 2a²=1 lub −2a²=1

	1
zatem a2=
	2

	1		1
zatem a=		oraz b=		lub to samo z minusami
	√2		√2

yyhy:

	1		1		1		1
z=		+		i lub z=−		−		i l
	√2		√2		√2		√2

piotr: z = a + bi ⁿ√z=|z|e^{arg(z)/n+2kπ/n}, k=0,..., n |z|=√a²+b² arg(z)=arctg(b/a)

Anna: co źle zrobiłem (x+iy)²=i x²+2xyi−y²=i x²−y²=0 2xy=1 x²+y²=√1²+0² 2x²=1+0 x²=1 x=1 lub x=−1 2*1*y=1

	1
y=
	2

2*(−1)*y=1

	−1
y=
	2

Anna: zrobiłam*

Anna: dobra już wiem

Anna: czy może jeszcze jakieś błędy zrobiłam ?

Mila: z²=i z=√i Wzory de Moivre'a: |i|=1

	π
φ=
	2

	π   +2kπ 2		π   +2kπ 2
zk=√1*(cos		+i sin		)
	2		2

gdzie: k=0,1

	π		π
z0=(cos		+i sin		)
	4		4

	√2		√2
z0=		+i
	2		2

	5π		5π
z1=(cos		+i sin		)⇔
	4		4

	√2		√2
z1=−		−i
	2		2

=====================

Anna: a zobacz na moj sposob gdybym nie zrobiła błędu to moim sposobem tez by wyszło? A i skąd wiesz że fi to jest π/2

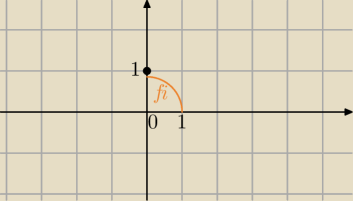
Mila: "i" to punkt na punkt( 0,1) zespolonej z=x+iy , x,y∊R x²+2xyi−y²=i x²−y²=0 2xy=1

	1
y=
	2x

x²+y²=1 x²−y²=0 −−−−−−−−−−−−− 2x²=1

	1
x2=
	2

	√2		√2
x=		lub x=−
	2		2

y=.. lub y= I masz to samo

kasia: dziekuje Mila

Mila: