Zadania typu maturalnego , wykaż że Lerus: Witam , prosiłbym o pomoc w tych 2 zadaniach. http://imgur.com/LYkGPrp Z góry dzięki za pomoc.

===: nie chce ci się wpisać treści ... a mnie nie chce się "biegać" po stronkach ... kopiować itp

Lerus: 6 Dane są punkty A=(1,3) B = (4,5). Wyznacz współrzędne takiego punktu C należącego do prostej y=7 by liczba d = /AC/ + /CB/ była najmniejsza. Odpowiedź uzasadnij 7 W trójkącie ABC dane są: /AC/ , /CB/. Wykaż , że jeżeli AD , BE i CF są wysokościami trójkąta

	/AC/ * /CB/
ABC oraz /AD/+/BE/=/CF/ to /AB/ =
	/AC/ + /CB/

Sorki myślałem że tak jest bardziej czytelnie

Krzysiek: c = <1;4>

Lerus: Krzyśku a można wiedzieć jak do tego doszedłeś ?

===: bzdura ... punkt o takich współrzędnych nie należy do prostej y=7

3Silnia&6: C lezy na prosej y=7, wiec ma wspolrzedne C=(x,7) AC = √(x−1)² + (7−3)² BC = ... jezeli |AC| + |BC| przyjmuje wartosc najmniejsza dla x=x₀, to dla x₀ wartosc |AC|² + |BC|² tez jest najmniejsza. |AC|² + |BC|² = (x−1)² + (7−3)² + ... − rownanie kwadratowe a>0, najmniejsza wartosc w wierzcholku.

3Silnia&6: do 7 proponuje rysunek i opisanie bokow AC =b, AB= c, BC=a, to samo z wysokosciami, a pozniej sam juz zobaczysz

===: C=(x_c, 7) |AC|=√(x_c−1)²+(7−3)²=√x_c²−2x_c+17 |BC|=√(x_c−4)²+(7−5)²=√x_c²−8x_c+20 twórz sumę i szukaj minimum

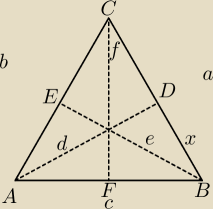
Lerus: Próbuję , ale Geometria to moja pięta Achillesowa i jakoś nie mam pomysłu wcale na to zadanie. Ze wzoru Pitagorasa na bok c= √(a−x)² + d² , i potem jakoś obliczyć x ?

	b*a
c=
	b+a

d+e=f

3Silnia&6: Robie.

3Silnia&6: Dane: a=|BC|, b= ,h_a=|AD|, h_b= ,h_c= ; dodatkowo c = |AB| h_a − wysokosc opuszczona na bok a, h_b,h_c odpowiednio na b i c. Z zadania mamy: h_a + h_b =h_c

	ab
A wykazac trzeba: c=
	a+b

	P		P		P
Pole = P = a*ha = b*hb = c*hc ⇒ ha =		; hb =		; hc =
	a		b		c

podstawiamy

	P		P		P
ha + hb =hc ⇒		+		=		/ P
	a		b		c

	1		1		1		a+b		ab
		+		=		=		⇒ c =
	a		b		c		ab		a+b

Lerus: Dziękuje bardzo za pomoc

3Silnia&6: