Wykaż, że równanie ma dokładnie jedno rozwiązanie rzeczywiste
Ludwik Montgomery:

Wykaż, że równanie x
7−7x+13 ma dokładnie jedno rozwiązanie rzeczywiste.
f'(x)= 7x
6−7
x
6=1
x=1 x=−1
Jak będzie tutaj wyglądał wykres pomocniczy funkcji?
Tak czy tak?
Od czego to zależy?
1 lut 20:43
PW: Co to jest u licha "wykres pomocniczy funkcji"? Przez taki żargon tracimy sens i zaczynamy
myśleć "jak to się robi" zamiast "co to znaczy".
Miejsca zerowe pochodnej mogą być punktami, w których f(x) osiąga ekstrema lokalne.
Rozstrzygnięcie, czy są, polega na ustaleniu, czy w sąsiedztwie tych punktów f'(x) zmienia
znak. W tym celu rysujemy wykres przybliżony wielomianu
x6−1 = (x3−1)(x3+1),
aby odczytać jego znaki z prawej i lewej strony punktów x1 = 1 oraz x2 = 1.
Równie dobrze można nic nie rysować, tylko o tym opowiedzieć.
Gdy już ustalimy gdzie jest ekstremum lokalne i czemu jest równe, to pewnie odpowiemy na
pytanie postawione w zadaniu.
1 lut 21:03
3Silnia&6:
f'(x) = 7x
6 − 7
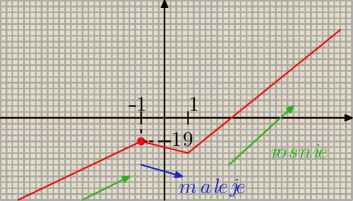
f'(x) < 0 ⇔ x ∊ (−1, 1) − funkcja malejaca dla x∊(−1,1), dla pozostalych rosnie.
f(−1) = −1 + 7 + 13 = 19 > 0
Czyli wykres funkcji wyglada jakos tak:
1 lut 21:05
3Silnia&6: Zle polczylem, wartosc funkcji dla x=−1

Ale schemat rozwiazania moze wygladac jak wyzej.
1 lut 21:07
Ludwik Montgomery: @PW dzięki, ale jak mam narysować ten wielomian?
Wiem, że muszę zacząć od prawej strony i od góry, ponieważ ma współczynnik a dodatni, ale co
dalej?
1 lut 21:12
PW: A wcale nie rysuj. Rozwiąż nierówność
(x3−1)(x3+1) > 0.
Wskazówka: Dla x < 1 lub dla x > 1 oba czynniki są ujemne, czyli iloczyn jest dodatni.
1 lut 21:25
Ludwik Montgomery: ehh, wychodzą mi jakieś bzdury.. może jeszcze jakaś podpowiedź?
1 lut 21:38
3Silnia&6:
Spróbuj sobie narysowac przyblizony wykres funkcji. Moze po prostu poprawie wczesniejszy zapis.
f(−1) = −1 + 7 + 13 = 19
f(1) = 1 − 7 + 13 = 14− 7 =7
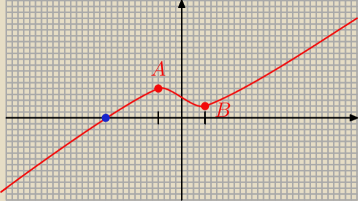
Oznacze A=(−1,19); B=(1,7)
Funkcja rosnie od −
∞ do −1, f(−1) >0, wiec mamy jedno miejsce zerowe (niebieski punkt). Pozniej
maleje do x=1, ale f(1) > 0, wiec nie ma miejsca zerowego, dalej rosnie, wiec wiadomo,ze nie
bedzie. Czyli wychodzi 1 rozwiazanie.
1 lut 21:46
 Wykaż, że równanie x7−7x+13 ma dokładnie jedno rozwiązanie rzeczywiste.
f'(x)= 7x6−7
x6=1
x=1 x=−1
Jak będzie tutaj wyglądał wykres pomocniczy funkcji?
Tak czy tak?
Od czego to zależy?
Wykaż, że równanie x7−7x+13 ma dokładnie jedno rozwiązanie rzeczywiste.
f'(x)= 7x6−7
x6=1
x=1 x=−1
Jak będzie tutaj wyglądał wykres pomocniczy funkcji?
Tak czy tak?
Od czego to zależy?
 f'(x) = 7x6 − 7
f'(x) < 0 ⇔ x ∊ (−1, 1) − funkcja malejaca dla x∊(−1,1), dla pozostalych rosnie.
f(−1) = −1 + 7 + 13 = 19 > 0
Czyli wykres funkcji wyglada jakos tak:
f'(x) = 7x6 − 7
f'(x) < 0 ⇔ x ∊ (−1, 1) − funkcja malejaca dla x∊(−1,1), dla pozostalych rosnie.
f(−1) = −1 + 7 + 13 = 19 > 0
Czyli wykres funkcji wyglada jakos tak:
 Ale schemat rozwiazania moze wygladac jak wyzej.
Ale schemat rozwiazania moze wygladac jak wyzej.
 Spróbuj sobie narysowac przyblizony wykres funkcji. Moze po prostu poprawie wczesniejszy zapis.
f(−1) = −1 + 7 + 13 = 19
f(1) = 1 − 7 + 13 = 14− 7 =7
Oznacze A=(−1,19); B=(1,7)
Funkcja rosnie od −∞ do −1, f(−1) >0, wiec mamy jedno miejsce zerowe (niebieski punkt). Pozniej
maleje do x=1, ale f(1) > 0, wiec nie ma miejsca zerowego, dalej rosnie, wiec wiadomo,ze nie
bedzie. Czyli wychodzi 1 rozwiazanie.
Spróbuj sobie narysowac przyblizony wykres funkcji. Moze po prostu poprawie wczesniejszy zapis.
f(−1) = −1 + 7 + 13 = 19
f(1) = 1 − 7 + 13 = 14− 7 =7
Oznacze A=(−1,19); B=(1,7)
Funkcja rosnie od −∞ do −1, f(−1) >0, wiec mamy jedno miejsce zerowe (niebieski punkt). Pozniej
maleje do x=1, ale f(1) > 0, wiec nie ma miejsca zerowego, dalej rosnie, wiec wiadomo,ze nie
bedzie. Czyli wychodzi 1 rozwiazanie.