 x−√x−1>0⇔
x−1>√x
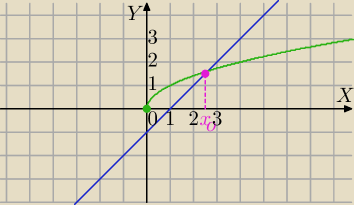
f(x)=x−1 , g(x)=√x szkicujemy wykresy obu funkcji.
Widać , że dla x>x0 wartości f(x) są większe od wartości funkcji g(x)
Należy znaleźć punkt przecięcia wykresów
x−1=√x , ponieważ √x≥0 to dziedziną równania będą liczby takie, że x−1≥0
D:
x≥1
x−1=√x / 2 (obie strony są nieujemne)
x2−2x+1=x
x2−3x+1=0
Δ=5
x−√x−1>0⇔
x−1>√x
f(x)=x−1 , g(x)=√x szkicujemy wykresy obu funkcji.
Widać , że dla x>x0 wartości f(x) są większe od wartości funkcji g(x)
Należy znaleźć punkt przecięcia wykresów
x−1=√x , ponieważ √x≥0 to dziedziną równania będą liczby takie, że x−1≥0
D:
x≥1
x−1=√x / 2 (obie strony są nieujemne)
x2−2x+1=x
x2−3x+1=0
Δ=5
| 3−√5 | 3+√5 | |||
x= | ∉D lub x= | |||
| 2 | 2 |
| 3+√5 | ||
x−√x−1>0 jest spełniona dla x> | ||
| 2 |