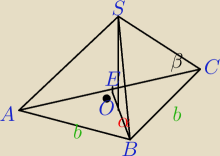
stereometria, trygonometria Archeolog: Podstawą ostrosłupa jest trójkąt równoramienny, wk tórym boki równe mają długość b, a kąt między nimi zawarty jest równy alfa. Oblicz objętość ostrosłupa, jeśli każda krawędź boczna tworzy z wysokością ostrosłupa kąt beta. No więc "zrobiłem" to zadanie, ale wynik mam zupełnie inny niż podają.

	α
Czy zakładając, że |AB|=|BC| = b można |AC| zapisać równaniem |AC| = 2 sin		* b ?
	2

	α
Bo |AE| = sin		i |AC| = 2|AE|...
	2

Wszystkie odpowiedzi jakie znajduje liczą twierdzeniem cosinusa, ale jak mamy podany kąt i bok to tak też powinno być poprawnie? odcinek OB to R, bo gdy mamy równe kąty to spodek wysokości ostrosłupa jest środkiem okręgu opisanego na tym trójkącie.

	2 sin U{α}2		|AC|
R liczyłem 2R =		( 2R =		)
	sin α		sin α

	α   b3*tg β* sin   2
Wynik końcowy mam V =
	6

Archeolog: dopiszę sobie że to zadanie 391 s. 69 z drugiej części zbioru Kiełbasy 2015 bo zapomnę gdzie tego w zeszycie szukać

Archeolog: Ktokolwiek? Siedzę i odświeżam.

Jack: gg <−−

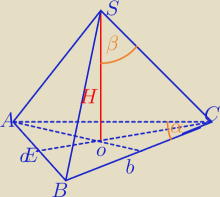iryt: I sposób: W ABC:

	1
PΔABC=		b2*sinα
	2

a²=b²+b²−2b²cosα a²=2b²−2b²cosα a=b*√2−2cosα Spodek wysokości pokrywa się ze środkiem okręgu opisanego na podstawie. Z tw. sinusów mamy

a
	=2R
sinα

	a
R=
	2sinα

|OC|=R W ΔSOC:

	|OC|
tgβ=
	H

	|OC|
H=
	tgβ

H=|OC|*ctgβ

	a
H=		*ctgβ
	2sinα

	1		1		a
V=		*		b2*sinα*		*ctgβ=
	3		2		2sinα

	1
V=		*b2*a*ctgβ
	12

Podstawiając za mamy:

	1		1
V=		*b2*b*√2−2cosα*ctgβ=		*b3*√2−2cosα*ctgβ
	12		12

Jeżeli obliczysz a z ΔCEB:

	α
a=2b*sin
	2

	1		α		1		α
Wtedy V=		*b2*2bsin		*ctgβ=		b3*sin		*ctgβ
	12		2		6		2

Ten wzór jest równoważny poprzedniemu. Przelicz .

Archeolog: Dzięki wielkie! Te V z drugiego sposobu wyszło mi gdy poprawiłem że ten kąt to 90−tg β i wtedy

	R
H =		i wyszło!
	tg β

Kacper: biorę