Graniastosłupy, przekrój i objętość
EMPE: Graniastosłup prawidłowy czworokątny przecięto płaszczyzną przechodzącą przez wierzchołek
podstawy i środek dokładnie jednej krawędzi bocznej. Otrzymany przekrój jest rombem o kącie
ostrym 60 stopni i boku 6. Oblicz objętość graniastosłupa.
Z góry dziękuję za pomoc i pozdrawiam.
1 lut 00:05
dero2005:
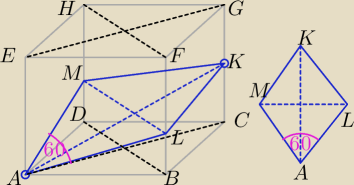
|KC| = |KG|
|AL| = |LK| = |KM| = |MA| = 6
|BD| = |AC| = |LM|
P
r = |AL|
2sin60
o = 18
√3 ⇒ pole rombu
W Δ ALM ∡A = 60
o, odcinki |AL|, |LM|, |AC| są równe i wynoszą 6
| | |AK|*|LM| | |
Pr = |
| = 36√3 ⇒ pole rombu |
| | 2 | |
|AK| = 6
√3
|CK| =
√|AK|2 − |AC|2 = 6
√2
|CG| = 2*|CK| = 12
√2
V = |AB|
2*|CG| = 216
√2 ⇒ objętość graniastosłupa
1 lut 17:52
Archeolog: dzięki wielki, skorzystałem
wcześniej jak sam liczyłem to założyłem głupio że kąt między A i K wynosi 45 stopni i się
posypało.
Nie zauważyłem, że |LM| = |DB|

5 lut 17:59
Kacper:
biorę

5 lut 18:24
Pawiuszek: Witam sorki ze odkopuje, ale mam pytanie dlaczego u gory na poczatku wyszlo pole rombu 18√3 a
pozniej przyrównane jest do 36√3

22 kwi 12:25
xxx: Zapomniał po prostu podzielić przez 2
9 sty 02:59
 |KC| = |KG|
|AL| = |LK| = |KM| = |MA| = 6
|BD| = |AC| = |LM|
Pr = |AL|2sin60o = 18√3 ⇒ pole rombu
W Δ ALM ∡A = 60o, odcinki |AL|, |LM|, |AC| są równe i wynoszą 6
|KC| = |KG|
|AL| = |LK| = |KM| = |MA| = 6
|BD| = |AC| = |LM|
Pr = |AL|2sin60o = 18√3 ⇒ pole rombu
W Δ ALM ∡A = 60o, odcinki |AL|, |LM|, |AC| są równe i wynoszą 6


