Okręgi
TT: Dane są okręgi o promieniach R i r styczne zewnętrznie. Do tych okręgów poprowadzono wspólną
styczna. Wykaż że pole czworokąta wyznaczonego przez środki tych okręgów i punkty styczności
jest równe (R+r)√R*r
31 sty 22:16
Eta:
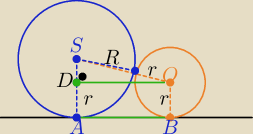
|DS|=R−r , |SO|= R+r |DO|=|AB|
Z twierdzenia Pitagorasa w trójkącie SDO
|DO|
2=|AB|
2= (R+r)
2−(R−r)
2 ⇒ |AB|
2= 4Rr ⇒ |AB|=2
√Rr
| | R+r | |
Pole trapezu ABOS : P= |
| *2√Rr= (R+r)*√Rr |
| | 2 | |
c.n.w
31 sty 22:28
kyrtap: to czasami nie z jakiejś matury zadanie chyba kiedyś rozwiązywałem ?

31 sty 22:30
TT: to z arkusza przygotowującego z Oficyny
31 sty 22:35
Eta:
A gdzie słowo........... dziękuję?

31 sty 22:36
TT: a oczywiście bardzo dziękuje miałem pisać

31 sty 22:40
Eta:

31 sty 22:41
 |DS|=R−r , |SO|= R+r |DO|=|AB|
Z twierdzenia Pitagorasa w trójkącie SDO
|DO|2=|AB|2= (R+r)2−(R−r)2 ⇒ |AB|2= 4Rr ⇒ |AB|=2√Rr
|DS|=R−r , |SO|= R+r |DO|=|AB|
Z twierdzenia Pitagorasa w trójkącie SDO
|DO|2=|AB|2= (R+r)2−(R−r)2 ⇒ |AB|2= 4Rr ⇒ |AB|=2√Rr



