Geometria Asia : Dana jest funkcja f(x)=x²+2x+4. Do wykresu funkcji poprowadzono styczne w punkktach A=(0,4) i B=(−3,7) przecinające się w punkcje C. Oblicz pole trójkąta ABC

Jerzy: najpierw znajdź równania stycznych

Asia : styczne będą miały to samo a

Jerzy: nie .... nie przecinałyby się

Asia: a=f'(x)

Jerzy: tak

Asia: f'(x)=2x+2 i teraz co muszę podstawić jako x₀

Jerzy: styczna: y = f'(x₀)(x−x₀) + f(x₀) i licz dla: x₀ = 0 oraz x₀ = −3

Asia: a wiem styczna 1: y=2x+4 styczna 2: −4 (x+3)+7

Jerzy: patrz na wzory wyżej

Asia: no dobrze chyba obliczone te styczne

Jerzy: pierwsza dobrze

kix: niestety źle

Asia: a i jak mam te styczne to podstawiam do układu równań te wzory stycznych i wychodzą mi współrzędne C a potem jak mam wszystkie punkty to moge obliczyc długości bokow i np z wzrou herona tak

Jerzy: druga też

Jerzy: teraz szukaj punkt przecięcia stycznych

Asia: {y=2x+4 {y=−4x−4 ⇒ 2x+4=−4x−4 ⇒x=−8/6=−4/3 y=4/3

kix: druga styczna y=−4x−5

Asia: mój błąd czyli x=−3/2 tak

kix: tak

Asia: y=−4 i 1/3

Asia: y=1

Asia: i co dalej

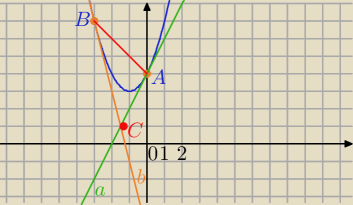
Mila: 1) f(x)=x²+2x+4 2) styczne w punktach A=(0,4) i B=(−3,7) przecinające się w punkcje C A i B należą do paraboli f'(x)=2x+2 a: y=f'(x₀)*(x−x₀)+f(x₀)⇔f'(0)=2, f(0)=4 a: y=2x+4 Druga styczna: f'(−3)=2*(−3)+2=−4, f(−3)=7 b: y=−4*(x+3)+7 b: y=−4x−5 3) punkt przecięcia stycznych −4x−5=2x+4

	3
x=−
	2

	3
y=2*(−		)+4=1
	2

	3
C=(−		,1)
	2

4) Pole ΔABC: Potrafisz dalej?

pytanie: dzięki dalej wystarczy odległosci policzyc

pytanie: dlaczego tam uzywamy pochodnych ?

5-latek: A jakie jest ogolne rownanie stycznej ?

Mila: W taki sposób możemy ustalić równania stycznych. A co nie miałeś pochodnych? Można skorzystać ,że prosta styczna ma dokładnie jeden punkt wspólny z parabolą. a: y=m*x+b i A∊a y=mx+4 x²+2x+4=mx+4 ⇔x²+2x−mx=0 x²+x*(2−m)=0 jedno rozwiązanie dla m=2 Styczna y=2x+4 druga styczna b: y=m*x+b i B=(−3,7)∊b policzysz dalej