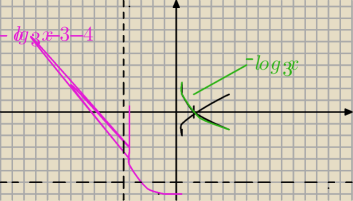
Wykres funkcji logarytmicznej broxy: Narysuj wykres funkcji f. Podaj dziedzinę tej funkcji, zbiór wartości oraz miejsca zerowe. Dla jakich argumentów wartości funkcji są nieujemne? a) f(x) = −log₃ (x+3) − 4 b) f(x) = | log (x−2) − 1| w pierwszym przykładzie zrobiłem wszystko ale nie zgadzają mi się asymptoty z odpowiedzią... Odpowiedź do przykładu to:

	80
D = (−3, ∞) , ZW = R+ , m,z = −2
	81

	80
f(x) ≥ 0 ⇔ x e (−3, −2		)
	81

Dlaczego zbiór wartości jest R+ ? Gdzie zrobiłem błąd

broxy: Proszę niech mi ktoś odpowie

	80
I dlaczego miejsce zerowe to −2
	81

broxy: wykres po przesunięciach to ten różowy

broxy: pomóżcie

Mila: f(x) = −log₃ (x+3) − 4 Taki wykres umiesz narysować?

broxy: Właśnie ten narysowałem na górze, różowy to wykres po przesunięciach.

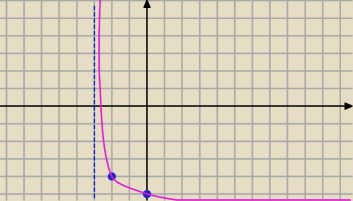
Mila: f(x)=−(log₃(x+3)+4) 1) rysujesz wykres y=log₃(x)→T_[−3,4]⇒ 2) y=log₃(x+3)+4⇒symetria względem OX 3) y=−log₃(x+3)−4 Wykres nie wychodzi, jest problem z funkcją rysuj.

broxy: No ok, i właśnie taki wykres narysowałem w zeszycie, teraz tylko chce wiedzieć dlaczego

	80
ZW = R+ a m.z = −2
	81

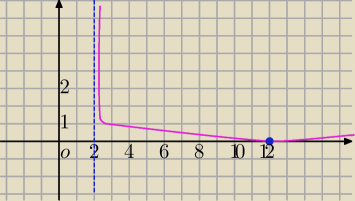
Mila: b) f(x) = | log (x−2) − 1| 1) y=log(x) 2) translacja wykresu o wektor [2,−1] 3) symetria względem tej części wykresu , która jest pod osią OX szkic ręczny

broxy: Dziękuję pięknie Mila, czy w punkcie a) miejsce zerowe bierze się z tego? −log₃ (x+3) − 4 = 0 log₃ (x+3) = −4 3⁻4 = x+3

	1		1		80
x+3 =		⇒ x		− 3 = −2
	81		81		81

Mila: Tak. a) Z_w=R b) |log(x−2)−1|=0 log(x−2)=1 x−2=10¹ x=12 co zaznaczyłam na wykresie . Zw=R₊

broxy: A w odpowiedzi do podpunktu a jest napisane że ZW = R+, dlaczego? Dlaczego nie od (+∞, −4) ? Pomijamy tą −4 bo nie ma ona znaczenia dla zbioru?