Pochodna funkcji a monotoniczność
Kapeć: Witam.
Wyznacz maksymalne przedziały monotoniczności funkcji f:
a) (1/4)x4 − 2x3 +5
b) (1/4)x4 − (1/3)x3 − (1/8)x2 + (1/4)x
I tak, liczę pochodne i wychodzą mi odwrotne wyniki, tzn.
a) funkcja f jest malejąca w przedziale <6, +∞) a rosnąca w przedziale (−∞, 6>
natomiast w odpowiedziach pisze:
funkcja f jest rosnąca w przedziale <6, +∞) a malejąca w przedziale (−∞, 6>
b) funkcja f jest malejąca w przedziale <−1/2, 1/2>, <1, +∞) a rosnąca w przedziale (−∞, −1/2>,
<1/2, 1>. W odpowiedziach:
funkcja f jest rosnąca w przedziale <−1/2, 1/2>, <1, +∞) a malejąca w przedziale (−∞, −1/2>,
<1/2, 1>
Błąd w odpowiedziach czy ja źle policzyłem?
31 sty 20:03
Kapeć: Można prosić o sprawdzenie?
Wystarczy mi odpowiedź czy komuś wyjdzie jak mi, czy jak w odpowiedziach.
31 sty 20:33
Janek191:
a)
f '(x) = x
3 − 6 x
2 = x
2*(x − 6)
Dla x < 6 jest f '(x) < 0 − f. jest malejąca
Dla x > 0 jest f '(x) > 0 − f. jest rosnąca
W x = 6 funkcja ma minimum
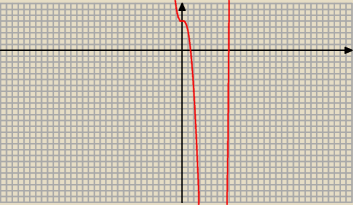
Patrz też na wykres

31 sty 21:09
 a)
f '(x) = x3 − 6 x2 = x2*(x − 6)
Dla x < 6 jest f '(x) < 0 − f. jest malejąca
Dla x > 0 jest f '(x) > 0 − f. jest rosnąca
W x = 6 funkcja ma minimum
Patrz też na wykres
a)
f '(x) = x3 − 6 x2 = x2*(x − 6)
Dla x < 6 jest f '(x) < 0 − f. jest malejąca
Dla x > 0 jest f '(x) > 0 − f. jest rosnąca
W x = 6 funkcja ma minimum
Patrz też na wykres