jak pies: Naszkicuj wykres funkcji f(x) = |(x − p)2 +2p| dla p = −2. Dla jakich wartości parametru p równanie f(x) = 6 ma dokładnie 3 rozwiązania? 2 czesc zad..dlaczego 2p=−6 ? dlaczego nie rozumiem i dlaczego nie np=6 ?

Jerzy: jeżeli tam jest: (x − 2)*2 + 2p , to nigdy nie będzie 3 rozwiazań, czyba,że jest: (x − p)² + 2p

pies: to drugie oczywisci ale odpowiedz

Jerzy: dokładnie trzy, gdy rzędna wierzchołka paraboli bedzie wynosiła − 6

pies: no wlasnie dlaczego −6 a dlaczego dla 6 ?takze ....co to rzedna ? to jest q ?

Jerzy: bo po odbiciu względem osi OX wierzchołek będzie miał rzędną 6

pies: nie rozumiem dlaczego po odbiciu

pies: ale kto go odbil

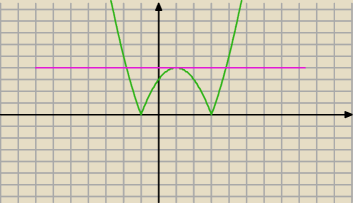
Jerzy: tu masz przykład wykresu funkcji: f(x) = |x² − 2x − 3I i równanie f(x) = 4 ma dokładnie 3 rozwiazania

pies: no ale to wiem co dalej

5-latek: Napisz najpierw wzor f(x) dla p=−2

pies: I(x+2)²−6I

pies: I(x+2)²−4I dla p=−2 i co ?

pies: pomozcie

5-latek: Widzisz ze to co jest w module to postac kanoniczna fukcji kwadratowej czyli możesz odczytac już wspolrzedne wierzchołka tej paraboli w srodku modulu x_w=p=−2 i y_w=q=−6 No to teraz y=(x+2)²−6 zamien na postac ogolna y= ax²+bx+c i policz miejsca zerowe tej funkcji Majac wspolrzedne wierzchołka i miejsca zerowe narysyjesz wykres funkcji y=x+2)²−6 Ale Ty masz f(x)=|(x+2)²−6| wiec te czesc wykresu y=(x+2)²−6 co jest pod osia Ox odbijasz nad os OX rysuj

5-latek: popraw sobie zamiast (−6) na (−4) bo zasugerowałem się Twoim wpisem

pies: nie rozumiem ...a moze byc tak ze −2=4 x=6 ⇒x=−3 /

5-latek: Masz narysować wykres tej funkcji f(x) dla p=−2 czego nie rozumiesz z tego co napisałem ?

pies: ale co to ma wpolnego z p=−2 ? bo to oddzielne zad ....a tak moze byc jak napisaelm to wogole ma sens?

5-latek: Z czy ma sens −2=4 ?

pies: no taka na krzyz wiesz ....skoro dla −2=4 to dla jakiegos x=6

5-latek: Przeciez nie zrobiles 1 części zadania czyli nie narysowales wykresu f(x) dla p=−2 Wiec to zrob najpierw

pies: przeciez wyzej jest narysowany

5-latek: A czy (x+2)²−4 rowna się x²−2x−3? Wiec czy to będzie ten sam wykres ?

pies: no chyba ej ...no wytlumacz dlaczego 5latku dlaczego jest=−6 a nie 6 skoro y= |(x − p)2 +2p|

pies: nie kaz rysowac bo nei umiem

pies: 5 latku

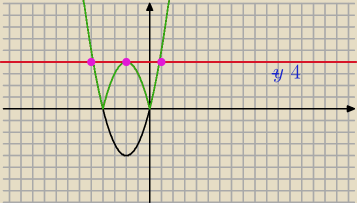
5-latek: No nie będzie ten sam wykres bo (x+2)²−4= x²+4x+4−4=x²+4x Wic czarny to wykres y=x²+4x wiec masz wierzchołek tej funkcji y_w=q=−4 Ty masz narysować wykres funkcji f(x)=|(x+2)²−4|= |x²+4x| (zielony ) Wie zobacz dla p=−2 f(x)=|(x−p)²+2p| ma 3 rozwiązania teraz f(x)=6 i maja być 3 rozwiązania czyli funkcja y=(x−p)²+2p (ta która jest w module musi mieć wspolrzedna y_w=q=−6 czyli 2p=−6 czyli p=−3 To dla p=−3 mam y=(x+3)²−6 (niebieski Treraz rysuje f(x)=|(x+3)²−6)| i f(x)=6 i ma mieć 3 rozwiązania Narysuje w osobnym poscie

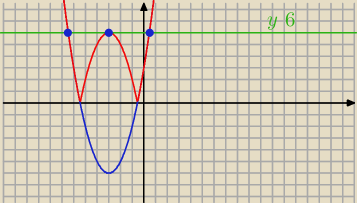
5-latek: bo zobacz dalej f(x)=|(x+3)²−6| (czerwony ) Widzisz ze masz 3 rozwiązania Widzisz ten caly pic polegana tym ze jak rysujesz y=|f(x)| to co [pd osia OX odbijasz nad os OX bo przecież wartość bezwzgledna nie może być ujemna

5-latek: I teraz tak żeby funkcja f(x)=|x−p)²+2p| miała wierzchołek w y_w=6 to funkcja (x−p)²+2p musi mieć wierzchołek w y=−6 dla tego je 2p=−6

utem: f(x)=(x−p)²+q to jest postać kanoniczna trójmianu kwadratowego (p,q) współrzędne wierzchołka paraboli W Twoim zadaniu f(x)=(x−p)²+2p to jest postać kanoniczna trójmianu kwadratowego, a=1 Parabola skierowana do góry (p,2p) współrzędne wierzchołka paraboli Aby równanie: |(x−p)²+2p|=6 miało trzy rozwiązania to wierzchołek o współrzędnych: (p, 2p) musi znajdować się pod osią OX, wtedy po odbiciu wykresu ( paraboli) względem osi OX będą 3 rozwiązania, jak na rysunku Jerzego i 5−latka. Jeżeli wierzchołek jest pod osią OX to 2p<0 |2p|=6⇔2p=6 ( nie odpowiada warunkom zadania) lub 2p=−6 ⇔p=−3 Wtedy masz wzór : f(x)=|(x−(−3))²+2*(−3)|⇔ f(x)=|(x+3)²−6| Jak wykonać taki wykres już tłumaczyłam. Czytaj dopóki nie zrozumiesz, potem możesz zadać pytanie. I jeszcze jedno: W(−3,−6) x=−3 odcięta y=−6 rzędna.

5-latek: Mysle ze kolega podziekuje za odpowiedz

pies: ej dlaczego dla p=−2 sa 3 rozwiazania ?

pies: nic nie zrozumialem z tego ...dlaczego musi byc pod osia zeby po odbiciu ...wszystko to bbez sensu

5-latek: No niestety ja to widze tak Dopóki nie nuczysz się rysować takich wykresow funkcji to bardzo trudno będzie CI to pojac Ja mysle ze Ty jesteś maturzysta wiec powinieneś już umiec . p=−2 wiec f(x)= |(x−(−2))²−2*(−2)|=|(x+2)²−4| Narysuj wykres tej funkcji

pies: nie nie nie cos sie uczepil tego p=−2 ....umiem rysowac tylko nie rozumiem tego wszystkiego dziwnych wnioskow ...i skad mam wiedziec ze dla p=−2 sa 3 rozwiazania?

pies: przeciez z rysunku nie odczytuje gdzie to p sie znajduje

5-latek: No wlasnie należy odczytac z wykresu A o p=−2 to TY pytales wiec odpisuje

pies: ja nie chce p=−2 ale dlaczego dla tego p =−2 sa 3 rozwiaazania?

pies: aaaa zadne takie jest zad: f(x) = |(x − p)² +2p| Dla jakich wartości parametru p równanie f(x) = 6 ma dokładnie 3 rozwiązania

pies: to ja zadlaenim pytanie ale nikt nie odpowie

pies: nie rozumiem po co to wszystko? no od(−2,+00) jest 2 rozwiazania

pies: jestem glupi eee dlaczego −2p=6

pies: ale po co ty wogle rysowalas na dole wierzcholek ?

Jerzy: bo tam leżał , przed nałożeniem modułu

pies: nie no ja nic z tego nie rozumiem ....jest wzor f(x) = |(x − p)² +2p| i f(x) = 6 ma 3 rozwiązania napiszesz w podpunktach takich ogolnych bardzo co po pokeli sie robi

Mila: Zostaw na razie to zadanie, rozwiązuj inne z funkcji, to w końcu opanujesz własności funkcji i wrócimy do tego zadania.

pies: ale to skomplokowane

Mila:

pies: ja wszystko rozumiem ale nie rozumiem ....no umiem to robic ale nie wiem dlaczego ...ej a dlaczego dla p = −2 sa 3 rozwiazania skad to odczytalas

Jerzy: na początek musisz rozumieć, jak powstaje wykres funkcji: y = If(x)I

pies: no wiem jak odbija sieej a dlaczego dla p = −2 sa 3 rozwiazania skad to odczytalas

pies: ej tylko to odpowiedz prosze juz nie bede pyπtal

Jerzy: już Ci to pisałem o 15:59 , aby po odbiciu wierzchołek miał rzędną 6 , to przed odbiciem musi mieć −6

5-latek: Ile to jest ? |2p|= |2*(−2)|= |−4|= ile ?

pies: ale nie o to pyπam dlaczego dla p=−2 sa 3 rozwiazania

5-latek: odpowiedz na moje pytanie

pies: ale to troche bez sensu dlaczego ta linia pozioma jest w y=6 0_o

kyrtap: nie lepiej tego typu zadania z wykresu odczytać? tak jak Pani Mila rysuje, wszystko na tacy widać jeśli wiemy że parametr p to rodzina prostych równoległych do osi OX

pies: ale dlaczego dla takiego wzoru ?|2p|= |2*(−2)|= |−4|

pies: ale p to ta kreska pozioma tak ? jak jest np x²+3=m to proste wiadomo dla jakiego m jest iles tam rozwiazan ale tu jest |(x−p)2+2p|=6 a nie tak jak wyzej

5-latek: Jestes naprawdę ciezki przypadek . Pytasz caly czas o p=−2 Podstaw do wzoru na f(x) p=−2 i narysuj wykres tej funkcji jeśli tego sam nie zrobisz to nie zrozumiesz tego . Trudno . ja ide spac bo jutro rano do pracy

pies: dobranoc slodkich snow

pies: ale ja nie mam obliczac dla p=−2

pies: ojoj lekam sie ale ja umiem wszystko robic rysowac itd..

pies: Dla p=−3 są trzy rozwiązania, nie widzisz na rysunku? no tego nie widac na rysunku dla p=−2 sa 2 rozwiazania

5-latek: Napisz na którym rysunku to widać

pies: na ostatnim rys.jest wykres niebieski ale nie wiem jak z tego odczytywac ile ma rozwiazan dla p...bo ja umiem tylko odczytywac jak jest np x²=p a tu tak nie jest

5-latek: czyli z godz 22:02 . Dobrze To teraz mamy taki wzor f(x)= |(x−p)²|+2p| Napisz jaki będzie wzor funkcji dla p=−2 i dla p=−3 czy te wzory będą takie same ? Jutro wrócimy do tego zadania

pies: ok ...dziekuje dobranoc

pies: 0 0

pies: dlaczego jak zmienie wartosc p na wartosc wierzcholka to f bedzie miec 3 rozwiazania

pies: i przeciez z wykresu nie da sei odczytac p

kyrtap: pies czasami warto coś zostawić i później do tego wrócić z innym spojrzeniem

pies: piesek ma sie poddac

5-latek: To zadanie ma dwa podpunkty . ja tak to rozumiem Jeden to dla f(x) =|(x−p)²+2p| narysować wykres tej funkcji dla p=−2 Wiec dla p=−2 f(x)= |(x+2)²−4| Teraz pytanie Czy wiesz jak narysować wykres funkcji f(x)=| (x+2)²−4| majac funkcje (x+2)²−4 ? czekam

pies: tak wiem jak mozna podstawiac liczby pod x albo odbic to co pod osia x

5-latek: To oznacza ze nie wiesz . mamy taka postac tej funkcji y=(x+2)²−4 Teraz pytanie jak to jest postac i co możemy z niej odczytac ?

5-latek: Podpowiem mamy postac ogolna , iloczynowa i kanoniczna . Która to jest ?

pies: kanoniczna

pies: ale mozna narysowac podstawiajac albo to co pod osia x odbic

5-latek: Dobrze . Postac kanoniczna Z postaci kanonicznej możemy odzcytac wspolrzedne wierzchołka paraboli mamy y=(x+2)²−4 (odczytaj te wspolrzedna czekam

pies: np p=−2 a q=−4

5-latek: Dobrze p=−2 i q=−4 mamy już jeden charakterystyczny punkt wykresu Brakuje jeszcze miejsc zerowych Obliczmy je (x+2)²−4=0 x²+4x+4−4=0 x²+4x=0 (rozwiąż to równanie

pies: x(x+4)=0 x=0 vx=−4

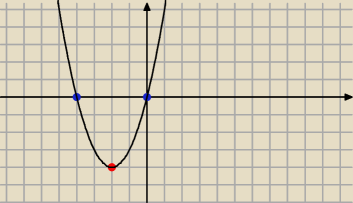
5-latek: Dobrze No to teraz możemy już narysować wykres funkcji y=(x+2)²−4 (czarny wykres to jest My jednak mamy narysować wykres funkcji f(x)= |(x+2)²−4| Ten czerwony punkt to wspolrzedne wierzchołka y=(x+2)²−4 czy wiesz gdzie on teraz powedruje (czyli jakie będą wspolrzedne wierzchołka dla f(x)= |(x+2)²−4| ?

pies: wsp w=4 no odbije sie to co pod osia do gory : −

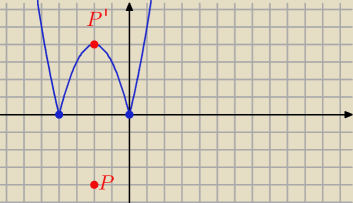
5-latek: No nie Punkt ma dwie wspolrzedne x_owa i y_owa czyli jeśli czerony punkt oznaczymy P=(−2,−4) Teraz jeśli go odbijemy względem osi OX to punkt symetryczny do niego będzie miał wspolrzedne P'=(−2,4) To teraz narysujmy na osobnym układzie wspolrzednych wykres funkcji f(x)= |(x+2)²−4| (niebieski wykres ) czyli to co było pod osia OX powedrowalo nad os OX Teraz dla tej niebieskiej funkcji napisz dla jakiego y istnieja 3 rozwiązania (czyli dla jakiego y wykres niebieski jest przeciety w 3 punktach ?

pies: dla y=4

5-latek: I bardzo dobrze No to teraz napisz ile wynosila wspolrzedna y_owa wierzcholka przed odbiciem ?

pies: −4

5-latek: Teraz się dobrze przypatrz temu rysunkowi Przed odbiciem y_w=−4 po odbiciu y_w=4 i ma 3 rozwiązania . czy już cos swita ? Pomysl czyli dla p=−2 f(x)=|(x−p)²+2p| ma 3 rozwiązania Teraz zobacz y_w= 2p=2*(−2)=−4 i po odbiciu dostajesz y_w'=4 Na tym zakończymy ten pierwszy podpunkt

pies: no ale co dalej ? 0−0

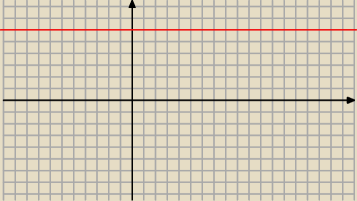
5-latek: Drugi podpunkt Dla jakiej wartości parametru p równanie f(x)=6 ma 3 rozwiązania czyli prosta y=6 ma przecinac wykres f(x)=|(x−p)²+2p| w 3 punktach Wiec wspolrzedna y_owa wierzchołka po odbiciu y_w=6 Wobec tego wspolrzedna y_w przed odbiciem musi wynosic y_w=−6 czyli y=(x−p)²+2p y_w=2p=−6 to p=−3 jeśli tego nie zrozumiesz to ja już nie potrafie inaczej CI tego wytlumaczyc

pies: no ok ale dlaej nie rozumiem dlaczego dla p= −2 sa 3 rozwiazania

pies: no bo przeciez dla p=−2 to jest cala funkcja....a tylko dla y=4 sa rozwiazania ...a nie dla p=−2 to jest takie pokrecone jaaaaaa

pies: wiem ze nic nie wiem nie bede meczyl juz ..dziekuje bardzo za pomoc